Somme cartésienne (graphe)
- Somme cartésienne (graphe)
-
Produit cartésien (graphe)
Le produit cartésien, ou somme cartésienne, est une opération sur deux graphes G et G' résultant en un graphe 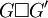 . Parler de produit ou de somme pour cette opération n'est pas une contradiction, mais une explication basée sur deux aspects différents : la construction peut se voir comme un produit, tandis que de nombreuses propriétés sont basées sur la somme.
. Parler de produit ou de somme pour cette opération n'est pas une contradiction, mais une explication basée sur deux aspects différents : la construction peut se voir comme un produit, tandis que de nombreuses propriétés sont basées sur la somme.
Construction

Produit cartésien de deux graphes.
Soient deux graphes G = (V,E) et G' = (V',E'). Le produit cartésien 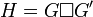 est défini comme suit :
est défini comme suit :
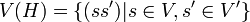 . Autrement dit, l'ensemble résultant des sommets V(H) est le produit cartésien V(G)xV(G').
. Autrement dit, l'ensemble résultant des sommets V(H) est le produit cartésien V(G)xV(G').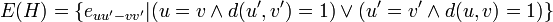 . Autrement dit, deux sommets sont voisins si les sommets dont ils sont issus étaient voisins dans l'un des deux graphes.
. Autrement dit, deux sommets sont voisins si les sommets dont ils sont issus étaient voisins dans l'un des deux graphes.
Propriétés
- Diamètre. Le diamètre DH du produit cartésien de G et G' est DH = DG + DG'.
- L'opération
 est commutative et associative.
est commutative et associative.
- Spectre. Le spectre d'un produit cartésien
 est {αi,βj}, où {αi} est le spectre de A et {βj} le spectre de B; autrement dit, le spectre est la somme de toutes les paires possibles[1]. Un exemple pratique est donné pour déduire le spectre de l'hypercube à partir des graphes dont il est le produit cartésien.
est {αi,βj}, où {αi} est le spectre de A et {βj} le spectre de B; autrement dit, le spectre est la somme de toutes les paires possibles[1]. Un exemple pratique est donné pour déduire le spectre de l'hypercube à partir des graphes dont il est le produit cartésien.
- Sommet-transitivité. Le produit cartésien
 est sommet-transitif si et seulement si A et B sont sommet-transitifs[2].
est sommet-transitif si et seulement si A et B sont sommet-transitifs[2].
- Connectivité. Le produit cartésien
 est connexe si et seulement si A et B sont connexes[2].
est connexe si et seulement si A et B sont connexes[2].
Utilisation
De nombreux graphes sont définis comme produits cartésiens, et on peut donc utiliser les propriétés de l'opération avec celles des graphes de base pour en déduire les propriétés du graphe obtenu :
- Le graphe de Hamming H(d,q) est le produit cartésien de d graphes complets Kq. Un cas particulier intéressant est l'hypercube Qd = H(d,2).
- La grille M(m,n) est obtenue par le produit cartésien[3] de chemins
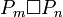 .
.
- La grille torique MT(m,n) est obtenue par le produit cartésien[3] de deux graphes cycles
 .
.
- Le prisme Ym,n est obtenu par le produit cartésien[4] d'un graphe cycle et d'un chemin
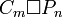 .
.
Références
- ↑ (en)Dragos M. Cvetkovic et Michael Doob et Horst Sachs - Spectra of Graphs, Heidelberg, Leipzig, 1994, (ISBN 3335004078).
- ↑ a et b Wilfried Imrich et Sandi Klavžar - Product Graphs: Structure and Recognition, Wiley, 2000, (ISBN 0-471-37039-8).
- ↑ a et b (fr) J-C. Bermond, P. Fraigniaud, A. Germa, M-C. Heydemann, E. Lazard, P. Michallon, A. Raspaud, D. Sotteau, M. Syska et D. Trystram - Communications dans les réseaux de processeurs, Masson, 1994, (ISBN 2225844100). Paru sous le pseudonyme Jean de Rumeur.
- ↑ (en) Eric W. Weisstein - Graph Cartesian Product, MathWorld--A Wolfram Web Resource, accédé le 17 février 2009.
Lectures complémentaires
(en) Wilfried Imrich, Sandi Klavžar et Douglas F. Rall - Topics in graph theory : graphs and their cartesian product, Wellesley, Mass. : A K Peters, 2008, (ISBN 9781568814292).
 Portail des mathématiques
Portail des mathématiques
Catégorie : Concept en théorie des graphes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Somme cartésienne (graphe) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Somme cartésienne de graphes — Produit cartésien (graphe) Le produit cartésien, ou somme cartésienne, est une opération sur deux graphes G et G résultant en un graphe . Parler de produit ou de somme pour cette opération n est pas une contradiction, mais une explication basée… … Wikipédia en Français
Graphe d'une relation — Correspondance et relation En algèbre générale (ou abstraite), le concept de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison. De manière informelle, une relation dans un … Wikipédia en Français
Produit cartésien (graphe) — Le produit cartésien, ou somme cartésienne, est une opération sur deux graphes G et G résultant en un graphe . Parler de produit ou de somme pour cette opération n est pas une contradiction, mais une explication basée sur deux aspects… … Wikipédia en Français
Ensemble-Produit — Produit cartésien Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes. En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble produit, est l ensemble… … Wikipédia en Français
Ensemble-produit — Produit cartésien Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes. En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble produit, est l ensemble… … Wikipédia en Français
Espace produit — Produit cartésien Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes. En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble produit, est l ensemble… … Wikipédia en Français
Produit cartesien — Produit cartésien Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes. En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble produit, est l ensemble… … Wikipédia en Français
Produit cartésien — Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes. En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble produit, est l ensemble de tous les… … Wikipédia en Français
Produit cartésien de graphes — Produit cartésien (graphe) Le produit cartésien, ou somme cartésienne, est une opération sur deux graphes G et G résultant en un graphe . Parler de produit ou de somme pour cette opération n est pas une contradiction, mais une explication basée… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
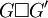 . Parler de produit ou de somme pour cette opération n'est pas une contradiction, mais une explication basée sur deux aspects différents : la construction peut se voir comme un produit, tandis que de nombreuses propriétés sont basées sur la somme.
. Parler de produit ou de somme pour cette opération n'est pas une contradiction, mais une explication basée sur deux aspects différents : la construction peut se voir comme un produit, tandis que de nombreuses propriétés sont basées sur la somme.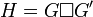 est défini comme suit :
est défini comme suit :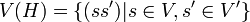 . Autrement dit, l'ensemble résultant des sommets V(H) est le produit cartésien V(G)xV(G').
. Autrement dit, l'ensemble résultant des sommets V(H) est le produit cartésien V(G)xV(G').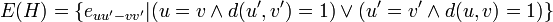 . Autrement dit, deux sommets sont voisins si les sommets dont ils sont issus étaient voisins dans l'un des deux graphes.
. Autrement dit, deux sommets sont voisins si les sommets dont ils sont issus étaient voisins dans l'un des deux graphes. est commutative et associative.
est commutative et associative. est {αi,βj}, où {αi} est le spectre de A et {βj} le spectre de B; autrement dit, le spectre est la somme de toutes les paires possibles[1]. Un exemple pratique est donné pour déduire le spectre de l'hypercube à partir des graphes dont il est le produit cartésien.
est {αi,βj}, où {αi} est le spectre de A et {βj} le spectre de B; autrement dit, le spectre est la somme de toutes les paires possibles[1]. Un exemple pratique est donné pour déduire le spectre de l'hypercube à partir des graphes dont il est le produit cartésien. est sommet-transitif si et seulement si A et B sont sommet-transitifs[2].
est sommet-transitif si et seulement si A et B sont sommet-transitifs[2]. est connexe si et seulement si A et B sont connexes[2].
est connexe si et seulement si A et B sont connexes[2].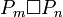 .
. .
.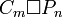 .
.
