Sinus intégral

Sinus intégral
Page d'aide sur l'homonymie Ne pas confondre avec la fonction sinus cardinal.
Tracé de Si(x) pour 0 \leqslant x \leqslant 8 \pi.

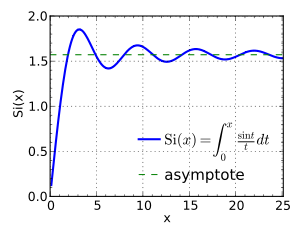
La fonction sinus intégral, notée Si, est une fonction spéciale de la physique mathématique introduite par Fresnel dans l'étude des vibrations lumineuses, est définie par l'intégrale :

\forall x \in \mathbb{R},\ \mathrm{Si}(x) = \int_{0} ^{x} \frac{\sin(t)}{t} \mathrm{d}t

où la fonction sin est la fonction sinus.

Sommaire

Historique

Cette fonction a été utilisée par Oscar Xavier Schlömilch (pour représenter certaines intégrales définies) avec la notation moderne Si(x) dès 1846. Une première tabulation de cette function (pour x=1,\ldots,10), due à Bretschneider, a été republiée par Schlömilch dans son "Analytische Studien" en 1848. Jean Denis Fenolio a publié en 1857 un mémoire suggérant plusieurs formules pour le calcul numérique de la fonction Si(x). Davide Besso a publié en 1868 une table de valeurs de Si(x) pour x multiple entier de π. Une tabulation plus précise que celles de Bretschneider et Besso a été publiée en 1870 par J. W. L. Glaisher, qui donne aussi un historique de l'utilisation de cette fonction dans la littérature mathématique. Des tables détaillées des fonctions cosinus intégral, exponentielle intégrale et sinus intégral ont été publiées en 1940 par la Federal Works Agency, sous la direction d'Arnold D. Lowan. L'introduction du volume 1 de ces tables contient (p. 26) une bibliographie des applications de ces fonctions en physique et en ingéniérie.

Propriétés

  • La fonction est continue, infiniment dérivable sur \mathbb{R}, et
\forall x \in \mathbb{R},\ \mathrm{Si}'(x) = \frac{\sin(x)}{x} = \mathrm{sinc}(x)

où sinc est la fonction sinus cardinal.

  • La fonction Si est développable en série entière sur \mathbb{R}, et on a
\forall x \in \mathbb{R},\ \mathrm{Si}(x) = \sum_{n=0}^{+\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!(2n+1)}

Ce développement permet d'étendre la fonction Si en une fonction analytique définie sur tout le plan complexe.

Voir aussi

Bibliographie

Liens


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sinus intégral de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Sinus integral — Sinus intégral La fonction sinus intégral, notée Si, est une fonction spéciale de la physique mathématique introduite par Fresnel dans l étude des vibrations lumineuses, est définie par . Propriétés La fonction est continue, infiniment dérivable… …   Wikipédia en Français

  • Sinus cardinal —      sinc (x): Sinus cardinal non normalisé      sinc (πx): Sinus cardinal normalisé En mathématiques, la fonc …   Wikipédia en Français

  • Sinus-Milieu — ist ein Begriff aus dem Marketing. Das Sinus Milieu beschreibt neben den geografischen, soziodemografischen und verhaltensbezogenen Segmentierungsvariablen die in den letzten Jahren immer wichtiger gewordene psychografische Variable. Die… …   Deutsch Wikipedia

  • Sinus lemniscatus — sl (schwarz) und Cosinus lemniscatus cl (blau), zum Vergleich der Sinus (hellgrau) Der lemniskatische Sinus oder sinus lemniscatus, abgekürzt sl, ist eine spezielle, von dem Mathematiker Carl Friedrich Gauß eingeführte mathematische Funktion. Der …   Deutsch Wikipedia

  • Sinus amplitudinis — In der Mathematik ist eine Jacobische elliptische Funktion eine von zwölf speziellen elliptischen Funktionen. Die Jacobischen elliptischen Funktionen haben einige Analogien zu den trigonometrischen Funktionen und finden zahlreiche Anwendungen in… …   Deutsch Wikipedia

  • Sinus Hyperbolicus und Kosinus Hyperbolicus — Eine Gerade durch den Nullpunkt schneidet die Hyperbel x2 − y2 = 1 im Punkt , wobei A für die Fläche zwischen der Geraden, ihrem Spiegelbild bezogen auf die x Achse und der Hyperbel steht. (Siehe …   Deutsch Wikipedia

  • Sinus integralis — Der Integralsinus ist ein Begriff aus der Mathematik und bezeichnet eine durch ein Integral gegebene Funktion. Joseph Liouville (1809 1882) bewies, dass der Kardinalsinus nicht elementar integrierbar ist. Der Integralsinus ist definiert als das… …   Deutsch Wikipedia

  • Logarithme intégral — En mathématiques, le logarithme intégral li est une fonction spéciale définie en tout nombre réel strictement positif x≠1 par l intégrale : Ici, ln désigne le …   Wikipédia en Français

  • Cosinus intégral — La fonction cosinus intégral, notée Ci est définie par l intégrale : où la fonction cos est la fonction cosinus. Propriétés La fonction est continue, infiniment dérivable sur , et …   Wikipédia en Français

  • Exponential integral — is a mathematical function of a single argument which has no established notation.DefinitionsFor real values of x , the exponential integral Ei( x ) can be defined as : mbox{Ei}(x)=int { infty}^xfrac{e^t}t,dt., The definition above can be used… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”