Signature algébrique

Signature algébrique

Signature (algèbre)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Signature.

En mathématiques, une signature pour une structure algébrique A sur un ensemble sous-jacent S est une liste d'opérations (avec leurs arités) qui caractérise A. Les signatures sont un concept important en algèbre universelle, et sont également employées en théorie des modèles, théorie des catégories et théorie des types.

Sommaire

Algèbre générale

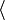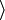Une signature est constituée de deux listes, encadrées par \langle et \rangle, dont les éléments sont séparés par des virgules.

  • Une liste commence par S suivi par les symboles des opérations qui caractérisent A. Une opération f d'arité n, où n est un entier naturel, est une fonction f: Sn→S. Des éléments distingués de S, comme un élement neutre ou un élement unité, sont considérés comme des opérations d'arité 0.
  • La seconde liste, composée des arités des opérations, est appelée le type de A. Les arités sont listées dans le même ordre que les opérations correspondantes.

Exemple

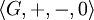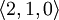un groupe additif sur G possède la signature \langle G,+,-,0 \rangle de type \langle 2,1,0 \rangle.

Algèbre linéaire

La signature d'une forme quadratique indique les signes devant les éléments de sa décomposition en carrés de formes linéaires indépendantes.
Cela se comprend mieux sur un exemple :

Exemple

Soit q(x,y,z) = 2yz + 3xz + xy.
On a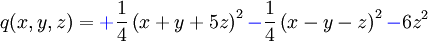 q(x,y,z) ={\color{Blue}+} \frac{1}{4} \left(x+y+5z\right)^2 {\color{Blue}-} \frac{1}{4} \left(x-y-z \right)^2 {\color{Blue}-} 6 z^2, avec 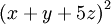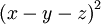\left(x+y+5z\right)^2 , \left(x-y-z \right)^2 et z2 linéairement indépendants.
Dès lors, la signature de q est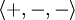 \langle +,-,- \rangle, notée aussi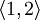 \langle 1,2 \rangle

Voir aussi

References

Monographie en ligne :

  • Burris, Stanley N., and H.P. Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3540905782. Voir en particulier pp. 22-24.
Ce document provient de « Signature (alg%C3%A8bre) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Signature algébrique de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Signature (arithmetique) — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et …   Wikipédia en Français

  • Signature (algebre) — Signature (algèbre) Pour les articles homonymes, voir Signature. En mathématiques, une signature pour une structure algébrique A sur un ensemble sous jacent S est une liste d opérations (avec leurs arités) qui caractérise A. Les signatures sont… …   Wikipédia en Français

  • Signature (arithmétique) — Pour les articles homonymes, voir Signature (homonymie). En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le …   Wikipédia en Français

  • Signature (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Article principal Signature Mathématiques signature d une structure algébrique, la liste de ses opérations avec leur arité, signature d une permutation,… …   Wikipédia en Français

  • Signature d'une permutation — Pour les articles homonymes, voir Signature (homonymie). En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c est à dire en une succession d échanges d éléments deux à deux. Une permutation paire est une… …   Wikipédia en Français

  • Structure (logique mathématique) — Pour les articles homonymes, voir Structure.  Ne doit pas être confondu avec Structure (mathématiques). En logique mathématique, plus précisément en théorie des modèles, une structure est un ensemble muni de fonctions et de relations… …   Wikipédia en Français

  • Plongement complexe — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et …   Wikipédia en Français

  • Plongement réel — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et …   Wikipédia en Français

  • Parité d'une permutation — Signature d une permutation En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c est à dire en une succession d échanges d éléments deux à deux. Une permutation paire est une permutation qui peut être… …   Wikipédia en Français

  • Permutation impaire — Signature d une permutation En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c est à dire en une succession d échanges d éléments deux à deux. Une permutation paire est une permutation qui peut être… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”