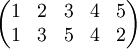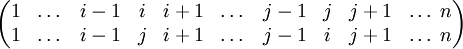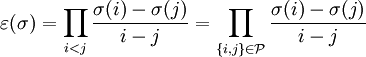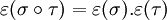Parité d'une permutation

Parité d'une permutation

Signature d'une permutation

En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c'est-à-dire en une succession d'échanges d'éléments deux à deux.

  • Une permutation paire est une permutation qui peut être exprimée comme le produit d'un nombre pair de transpositions ;
  • une permutation impaire est une permutation qui peut être exprimée comme le produit d'un nombre impair de transpositions.

La signature d'une permutation vaut 1 si celle-ci est paire, -1 si elle est impaire. L'application signature constitue un morphisme de groupes. Elle intervient en algèbre multilinéaire, notamment pour le calcul des déterminants.

Sommaire

Définition de la signature

Soit une permutation σ. La définition traditionnelle de la parité de σ se fait par le comptage des inversions.

Définition

Soient i<j deux éléments distincts compris entre 1 et n. On dit que la paire {i,j} est en inversion pour σ quand σ(i) > σ(j).

Une permutation est dite paire quand elle présente un nombre pair d'inversions, impaire sinon.

Exemple
Soit la permutation
\begin{pmatrix} 1&2&3&4&5\\1&3&5&4&2\end{pmatrix}
La paire {1,2} n'est pas en inversion puisque les images de 1 et 2 sont rangées dans le même ordre. Il en est de même pour 1 et 3. La liste des paires en inversion est {2,5}, {3,4}, {3,5}, {4,5}. Il y en a quatre, donc la permutation est paire.

Par définition, la signature d'une permutation paire est 1, celle d'une permutation impaire est -1.

Une transposition est impaire

Toute transposition est une permutation impaire. En effet en notant i et j, i<j, les termes échangés par la transposition, celle-ci s'écrit

\begin{pmatrix} 1&\dots&i-1&i&i+1&\dots &j-1&j&j+1&\dots\; n\\ 1&\dots & i-1&j&i+1&\dots &j-1&i&j+1&\dots\; n\end{pmatrix}

Les paires en inversion sont les paires de la forme {i,k} avec k compris entre i+1 et j et celles de la forme {k,j} avec k compris entre i+1 et j-1. Au total, il y a un nombre impair d'inversions, et l'imparité de la permutation en découle.

Une formule pour la signature

On note 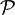{\mathcal P} l'ensemble des paires d'éléments compris entre 1 et n (il y en a n(n-1)/2). Une permutation σ a pour signature

\varepsilon(\sigma)=\prod\limits_{i<j} \frac{\sigma(i)-\sigma(j)}{i-j} =\prod\limits_{\{i,j\}\in {\mathcal P}} \frac{\sigma(i)-\sigma(j)}{i-j}
Démonstration
Appelons P ce produit. Examiner tous les couples (i,j) avec i<j revient à examiner toutes les paires {i,j}. Pour chacune d'elles, le terme qui se trouve dans le produit a un signe négatif si la paire est en inversion, positif sinon. Ceci montre que le signe de P est bien celui de la signature. Enfin, par bijectivité de σ, les termes σ(i)-σ(j) du numérateur sont, au signe près, les mêmes que les i-j du dénominateur. Ceci montre que la valeur absolue de P vaut 1 et permet de conclure.

Cette formule a un certain intérêt algébrique mais ne permet pas un calcul efficace de la signature dans la pratique. En effet par rapport au simple comptage des inversions s'ajoute la multiplication et la division par un certain nombre d'entiers.

Signature d'un produit

Les permutations vérifient une règle des signes pour le produit : le produit de deux permutations paires est pair, de deux permutations impaires est pair, le produit d'une permutation paire et d'une impaire est impair. En utilisant la signature, cela se résume par la formule

\varepsilon(\sigma\circ\tau)=\varepsilon(\sigma).\varepsilon(\tau)
Démonstration
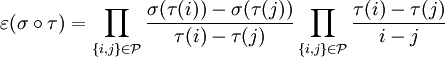
\varepsilon(\sigma\circ \tau )=\prod\limits_{\{i,j\}\in {\mathcal P}} \frac{\sigma(\tau(i))-\sigma(\tau(j))}{\tau(i)-\tau(j)} \prod\limits_{\{i,j\}\in {\mathcal P}} \frac{\tau(i)-\tau(j)}{i-j}
Dans le deuxième facteur du second membre, on reconnaît directement une signature. Pour le premier, il faut au préalable réindexer en posant {i',j'}={τ(i),τ(j)}, on y reconnaît alors également une signature.

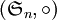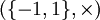En termes algébriques : la signature est un morphisme de groupes du groupe symétrique (\mathfrak S_n,\circ) dans \left(\{-1,1\},\times\right). L'ensemble des permutations paires forme le groupe alterné, noyau de ce morphisme. Enfin la permutation inverse de σ a la même signature que σ.

Calcul d'une signature

En corollaire des résultats précédents,

  • une permutation est paire si et seulement si elle peut être exprimée comme le produit d'un nombre pair de transpositions ;
  • une permutation est impaire si et seulement si elle peut être exprimée comme le produit d'un nombre impair de transpositions

et ces deux cas s'excluent mutuellement.

Le calcul de la signature par la décomposition en produit de transpositions est beaucoup plus efficace que l'application de la définition initiale ; en effet pour une permutation de 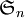{\mathfrak S}_n cette décomposition demande au plus n-1 opérations, contre n(n-1)/2 pour la définition.

Exemples
l'identité est une permutation paire ;
une transposition est une permutation impaire ;
une permutation circulaire est paire si le nombre d'éléments est impair ; elle est impaire si le nombre d'éléments est pair.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Signature d%27une permutation ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Parité d'une permutation de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Signature d'une permutation — Pour les articles homonymes, voir Signature (homonymie). En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c est à dire en une succession d échanges d éléments deux à deux. Une permutation paire est une… …   Wikipédia en Français

  • Parité (mathématiques) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques, la parité a plusieurs significations selon le contexte : en arithmétique élémentaire, la notion de parité est utilisée pour… …   Wikipédia en Français

  • Permutation circulaire — En mathématiques, une permutation circulaire ou cycle est un cas particulier de permutation. Une permutation circulaire agit comme un décalage circulaire pour un certain nombre d éléments, et laisse tous les autres inchangés. Les permutations… …   Wikipédia en Français

  • Permutation — En mathématiques, la notion de permutation exprime l idée de réarrangement d objets discernables. Une permutation de n objets distincts rangés dans un certain ordre, correspond à un changement de l ordre de succession de ces n objets. La… …   Wikipédia en Français

  • Permutation impaire — Signature d une permutation En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c est à dire en une succession d échanges d éléments deux à deux. Une permutation paire est une permutation qui peut être… …   Wikipédia en Français

  • Permutation paire — Signature d une permutation En mathématiques, les permutations peuvent se décomposer en un produit de transpositions, c est à dire en une succession d échanges d éléments deux à deux. Une permutation paire est une permutation qui peut être… …   Wikipédia en Français

  • Permutable — Permutation En mathématiques, la notion de permutation exprime l idée de réarrangement d objets discernables. Une permutation de n objets distincts rangés dans un certain ordre, correspond à un changement de l ordre de succession de ces n objets …   Wikipédia en Français

  • Matrice génératrice — Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires. Elle correspond à la matrice de l application linéaire de E l espace vectoriel des messages à communiquer dans F, l espace vectoriel contenant… …   Wikipédia en Français

  • Groupe Alterné — En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est composé des… …   Wikipédia en Français

  • Groupe alterne — Groupe alterné En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”