Plongement réel
- Plongement réel
-
Signature (arithmétique)
En théorie algébrique des nombres, la signature d'un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et r2 le nombre de couples de plongements complexes conjugués du corps K ; un plongement, injection dans le corps algébriquement clos des nombres complexes, est considéré réel s'il est à valeurs dans le sous-corps des nombres réels, et complexe sinon.
C'est un fait classique en théorie des corps que chaque plongement complexe admet un plongement complexe conjugué, ainsi que la relation r1+2r2=n, où n est le degré du corps K sur le corps des nombres rationnels.
La signature d'un corps de nombres intervient dans de nombreuses formules arithmétiques, comme le théorème des unités de Dirichlet, ou le dénombrement des 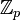 -extensions linéairement indépendantes, en théorie d'Iwasawa.
-extensions linéairement indépendantes, en théorie d'Iwasawa.
Références
- (en) Jürgen Neukirch, Algebraic number theory [détail des éditions]
- Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie algébrique des nombres
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Plongement réel de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Plongement complexe — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et … Wikipédia en Français
Theoreme de plongement de Whitney — Théorème de plongement de Whitney En topologie différentielle, le théorème de plongement de Whitney fait le lien entre les notions de variété abstraite et de sous variété de l espace vectoriel réel Rn : toute variété différentielle de… … Wikipédia en Français
Théorème de plongement de whitney — En topologie différentielle, le théorème de plongement de Whitney fait le lien entre les notions de variété abstraite et de sous variété de l espace vectoriel réel Rn : toute variété différentielle de dimension m peut être plongée dans l… … Wikipédia en Français
Théorème de plongement de Whitney — En topologie différentielle, le théorème de plongement de Whitney fait le lien entre les notions de variété abstraite et de sous variété de l espace vectoriel réel Rn : toute variété différentielle de dimension m peut être plongée dans l… … Wikipédia en Français
Corps Totalement Réel — En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière équivalente, K est… … Wikipédia en Français
Corps de nombres totalement réel — Corps totalement réel En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière… … Wikipédia en Français
Corps totalement reel — Corps totalement réel En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière… … Wikipédia en Français
Corps totalement réel — En mathématiques et en théorie des nombres, un corps de nombres K est dit totalement réel si pour chaque plongement de K dans l ensemble des nombres complexes, l image se trouve dans l ensemble des nombres réels. De manière équivalente, K est… … Wikipédia en Français
Theoreme de Minkowski — Théorème de Minkowski En mathématiques, le théorème de Minkowski est un résultat concernant la géométrie des réseaux. Il relie le nombre de points du réseau contenu dans une partie convexe symétrique au volume fondamental du réseau. Ce théorème… … Wikipédia en Français
Théorème de Minkowski — En mathématiques, le théorème de Minkowski est un résultat concernant la géométrie des réseaux. Il relie le nombre de points du réseau contenu dans une partie convexe symétrique au volume fondamental du réseau. Ce théorème est utilisé en théorie… … Wikipédia en Français
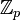 -extensions linéairement indépendantes, en théorie d'Iwasawa.
-extensions linéairement indépendantes, en théorie d'Iwasawa.