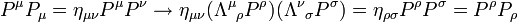Scalaire de Lorentz

Scalaire de Lorentz

Invariance de Lorentz

Dans le cadre de la relativité restreinte (qui reste valable aussi en relativité générale), une quantité est dite invariante de Lorentz, on dit aussi scalaire de Lorentz, ou invariant relativiste, lorsqu'elle n'est pas modifiée sous l'application d'une transformation de Lorentz. Cela revient à dire que sa valeur est la même dans tous les référentiels galiléens.

Le premier exemple de quantité invariante de Lorentz est la métrique de Minkowski[1] 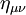\eta_{\mu\nu}\,. Si on considère une transformation de Lorentz représentée par 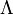\Lambda\,[2], alors on a par définition des transformations de Lorentz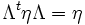

\Lambda^t\eta\Lambda=\eta \,

si on utilise la notation matricielle, ou

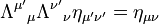
{\Lambda^{\mu'}}_\mu{\Lambda^{\nu'}}_\nu\eta_{\mu' \nu'}=\eta_{\mu\nu} \,

si on adopte la notation d'indices plus commune en physique. On a adopté pour cette dernière la convention de sommation d'Einstein qui somme implicitement selon les quatre directions tout indice apparaissant à la fois en haut et en bas d'une expression.

A partir de cette quantité invariante fondamentale on peut en construire d'autres. Par exemple si on considère le quadrivecteur d'énergie-impulsion [3],

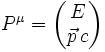
P^{\mu}= \begin{pmatrix} E\\ \vec{p}\,c \end{pmatrix} \,

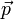constitué de l'énergie E\, et de l'impulsion \vec{p}\,. Il n'est pas invariant de Lorentz car il se transforme de la façon suivante [4]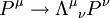

P^\mu\rightarrow{\Lambda^\mu}_\nu P^\nu \,

Mais par contre on peut construire la quantité quadratique suivante par contraction de ce quadrivecteur en utilisant la métrique

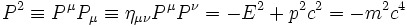
P^2\equiv P^{\mu}P_{\mu}\equiv\eta_{\mu\nu}P^{\mu}P^{\nu}=-E^2+p^2c^2=-m^2c^4 \,

qui définit la masse en relativité restreinte. Cette quantité est un invariant de Lorentz, car si Pμ subit une transformation de Lorentz, la quantité PμPμ devient :

P^\mu P_\mu=\eta_{\mu\nu}P^\mu P^\nu\rightarrow\eta_{\mu\nu}({\Lambda^\mu}_\rho P^\rho)({\Lambda^\nu}_\sigma P^\sigma)=\eta_{\rho\sigma}P^\rho P^\sigma=P^\rho P_\rho

où on a utilisé l'invariance de la métrique énoncée au début de cette page pour l'avant-dernière étape du calcul. Comme μ et ρ sont des indices muets, on a bien retrouvé la norme du quadrivecteur P, qui est donc une grandeur invariante. [5]

Dans cette démonstration, nous n'avons à aucun moment utilisé l'expression explicite de P, ce qui signifie que la norme de n'importe quel quadrivecteur est une grandeur conservée par les transformations de Lorentz.

Le fait qu'une quantité soit invariante permet d'obtenir des résultats intéressants en choisissant des référentiels particuliers. Par exemple, si on considère le cas d'une particule de masse non-nulle 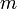m\, alors on peut considérer le référentiel de repos dans lequel on a 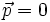\vec{p}=0\,. On obtient alors la célèbre identité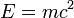

E=mc^2 \,

Par contre dans le cas d'une particule de masse nulle, comme le photon, il n'est pas possible de trouver un tel référentiel mais on a alors la relation

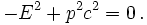
-E^2+p^2c^2=0 \,.

Notes

  1. ↑ On utilise par la suite ici la signature 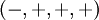(-,+,+,+)\, pour la métrique.
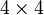  2. ↑ C'est une matrice 4\times 4.
  3. ↑ Lorsqu'on se place a priori dans le cadre de la mécanique relativiste il est d'usage d'oublier le préfixe quadri et de parler plus simplement de vecteur ou dimpulsion.
  4. ↑ c'est la définition même d'un vecteur
  5. ↑ Invariant sous-entend 'par transformation de Lorentz'. Ne pas confondre avec conservé qui signifie constant dans le temps. La masse d'une particule élémentaire est invariante. En l'absence d'actions extérieures, son vecteur énergie-impulsion est conservé (mais pas invariant)

Voir aussi


  • Portail de la physique Portail de la physique
Ce document provient de « Invariance de Lorentz ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Scalaire de Lorentz de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Scalaire — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 En tant que notion commune aux mathématiques et à la physique 1.1 Exemples …   Wikipédia en Français

  • Covariance De Lorentz — En relativité restreinte, une quantité est dite covariante de Lorentz lorsque ses composantes forment une représentation du groupe de Lorentz. Par exemple le temps propre se transforme de façon particulièrement simple puisqu il est invariant sous …   Wikipédia en Français

  • Covariance de lorentz — En relativité restreinte, une quantité est dite covariante de Lorentz lorsque ses composantes forment une représentation du groupe de Lorentz. Par exemple le temps propre se transforme de façon particulièrement simple puisqu il est invariant sous …   Wikipédia en Français

  • Covariance de Lorentz — En relativité restreinte, une quantité est dite covariante de Lorentz lorsque ses composantes forment une représentation du groupe de Lorentz. Par exemple le temps propre se transforme de façon particulièrement simple puisqu il est invariant sous …   Wikipédia en Français

  • Invariance De Lorentz — Dans le cadre de la relativité restreinte (qui reste valable aussi en relativité générale), une quantité est dite invariante de Lorentz, on dit aussi scalaire de Lorentz, ou invariant relativiste, lorsqu elle n est pas modifiée sous l application …   Wikipédia en Français

  • Invariance de lorentz — Dans le cadre de la relativité restreinte (qui reste valable aussi en relativité générale), une quantité est dite invariante de Lorentz, on dit aussi scalaire de Lorentz, ou invariant relativiste, lorsqu elle n est pas modifiée sous l application …   Wikipédia en Français

  • Invariant de Lorentz — Invariance de Lorentz Dans le cadre de la relativité restreinte (qui reste valable aussi en relativité générale), une quantité est dite invariante de Lorentz, on dit aussi scalaire de Lorentz, ou invariant relativiste, lorsqu elle n est pas… …   Wikipédia en Français

  • Invariance de Lorentz — Dans le cadre de la relativité restreinte (qui reste valable aussi en relativité générale), une quantité est dite invariante de Lorentz, on dit aussi scalaire de Lorentz, ou invariant relativiste, lorsqu elle n est pas modifiée sous l application …   Wikipédia en Français

  • Transformation de lorentz — Cet article présente les transformations de Lorentz sous un aspect technique. Le lecteur désireux d obtenir des informations physiques plus générales à ce sujet pourra se référer à l article relativité restreinte. Les transformations de Lorentz… …   Wikipédia en Français

  • Transformations de Lorentz — Transformation de Lorentz Cet article présente les transformations de Lorentz sous un aspect technique. Le lecteur désireux d obtenir des informations physiques plus générales à ce sujet pourra se référer à l article relativité restreinte. Les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”