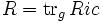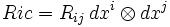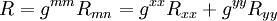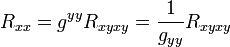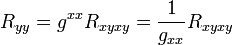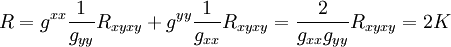Scalaire de Ricci

Scalaire de Ricci

Courbure scalaire

En géométrie différentielle, la courbure scalaire (ou courbure de Ricci, ou scalaire de Ricci) est l'outil le plus simple pour décrire la courbure d'une variété riemannienne. Il assigne à chaque point d'une variété riemannienne un simple nombre réel caractérisant la courbure intrinsèque de la variété en ce point.

Dans un espace à deux dimensions, la courbure scalaire caractérise complètement la courbure de la variété. En dimension ≥ 3, cependant, il n'y suffit pas et d'autres outils sont nécessaires.

La courbure scalaire, habituellement dénotée R est définie comme la trace du tenseur de Ricci relativement à la métrique.

R = \mbox{tr}_g\,Ric

On peut aussi écrire

R = gijRij,

avec

Ric = R_{ij}\,dx^i\otimes dx^j

Scalaire de Ricci en deux dimensions et en coordonnées de Riemann

Le scalaire de Ricci R ou Ric s'obtient à partir du tenseur de Ricci par la relation générale, appliquée à une surface[1] :

\left. R = g^{mm} R_{mn} = g^{xx} R_{xx} +g^{yy} R_{yy}\right.

En utilisant les relations entre composantes directes et inverses de la métrique ainsi que les relations entre les tenseurs de Riemann Rxyxy et de Ricci de composantes Rxx et Ryy qui s'écrit alors, en deux dimensions[2] :

R_{xx} = g^{yy}R_{xyxy} = \frac{1}{g_{yy}}R_{xyxy}
R_{yy} =g^{xx}R_{xyxy} = \frac{1}{g_{xx}}R_{xyxy}

on obtient la relation entre le scalaire de Ricci et la courbure de Gauss:

R = g^{xx}\frac{1}{g_{yy}}R_{xyxy}+g^{yy}\frac{1}{g_{xx}}R_{xyxy}=\frac{2}{g_{xx}g_{yy}}R_{xyxy}=2K

En deux dimensions, c’est-à-dire pour une surface, le scalaire de Ricci est le double de la courbure de Gauss K (au signe près selon la convention utilisée).

Notes et références

  1. ↑ En toute rigueur on devrait utiliser ici u et v au lieu de x et y car il s'agit de coordonnées de Gauss (voir Tenseur de Riemann)
  2. ↑ Bernard Schaeffer, Relativités et quanta clarifiés, Publibook, 2007

Voir aussi

Hakim, R, Gravitation relativiste, EDP Sciences, 2001

Riemannian geometry

  • Portail de la physique Portail de la physique
Ce document provient de « Courbure scalaire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Scalaire de Ricci de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Scalaire de courbure — Courbure scalaire En géométrie différentielle, la courbure scalaire (ou courbure de Ricci, ou scalaire de Ricci) est l outil le plus simple pour décrire la courbure d une variété riemannienne. Il assigne à chaque point d une variété riemannienne… …   Wikipédia en Français

  • Ricci —  Cette page d’homonymie répertorie des personnes (réelles ou fictives) partageant un même patronyme. Patronymes Ricci est un patronyme italien, porté par les personnes suivantes, de nationalité italienne ou d origine italienne : Ricci,… …   Wikipédia en Français

  • Courbure Scalaire — En géométrie différentielle, la courbure scalaire (ou courbure de Ricci, ou scalaire de Ricci) est l outil le plus simple pour décrire la courbure d une variété riemannienne. Il assigne à chaque point d une variété riemannienne un simple nombre… …   Wikipédia en Français

  • Courbure de Ricci — Courbure scalaire En géométrie différentielle, la courbure scalaire (ou courbure de Ricci, ou scalaire de Ricci) est l outil le plus simple pour décrire la courbure d une variété riemannienne. Il assigne à chaque point d une variété riemannienne… …   Wikipédia en Français

  • Courbure scalaire — En géométrie différentielle, la courbure scalaire (ou courbure de Ricci, ou scalaire de Ricci) est l outil le plus simple pour décrire la courbure d une variété riemannienne. Il assigne à chaque point d une variété riemannienne un simple nombre… …   Wikipédia en Français

  • Flot de Ricci — Programme de Hamilton Le programme de Hamilton est une idée de « plan d attaque », due à Richard Hamilton, de certains problèmes en topologie des variétés, notamment la célèbre conjecture de Poincaré. Nous allons essayer de décrire ici …   Wikipédia en Français

  • Tenseur de ricci — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de Ricci — Dans le cadre de la théorie de la Relativité générale[1], le champ de gravitation est interprété comme une déformation de l espace temps. Cette déformation est exprimée à l aide du tenseur de Ricci, dont le nom a été attribué d après son… …   Wikipédia en Français

  • Métrique de Poincaré — En mathématiques, et plus précisément en géométrie différentielle, la métrique de Poincaré, due à Henri Poincaré, est le tenseur métrique décrivant une surface de courbure négative constante. C est la métrique naturelle utilisée pour des calculs… …   Wikipédia en Français

  • Programme de Hamilton — Le programme de Hamilton est une idée de « plan d attaque », due à Richard Hamilton, de certains problèmes en topologie des variétés, notamment la célèbre conjecture de Poincaré. Cet article tente de décrire les raisons d être de ce… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”