- Resolution d'equations differentielles par quadrature
-
Résolution d'équations différentielles par quadrature
Le problème de la résolution par quadrature pour une équation différentielle consiste à rechercher une écriture explicite pour les solutions de celle-ci. Malheureusement, s'il existe un certain nombre d'équations classiques présentant des procédés de résolution systématique, une telle résolution est impossible en général.
Cette question est motivée par la confrontation à une série d'exemples provenant pour grande partie de l'application des mathématiques à la physique, la biologie, ... (seconde loi de Newton , équation de la chaleur, équation des ondes, ...).
De ce fait, un grand nombre de méthodes de résolution numérique des équations différentielles ont été développées pour obtenir des solutions approchées. Une autre direction d'analyse, initiée par Henri Poincaré en 1880, et qui s'imposera à partir du début du XXe siècle, est l'étude qualitative des équations différentielles[réf. nécessaire].
Théorie de la résolution
La résolution explicite vise à écrire sous une forme analytique la solution à une équation différentielle. Plus précisément, étant donné une équation de la forme :
- F(t,x(t),x'(t),...,x(n)(t)) = 0
où x(t) varie dans un espace vectoriel topologique réel ou complexe E, on cherche une expression de x(t) suivant une condition initiale x(t0) et de la variable réelle t ne faisant intervenir que :
- Des opérations algébriques ;
- Des fonctions élémentaires ;
- Des quadratures ;
- Des inversions de difféomorphismes.
Le problème de la résolution explicite ne suppose pas a priori l'existence ou l'unicité d'une ou des solution(s) recherchée(s).
Il peut être prouvé qu'une équation différentielle générique ne peut pas être résolue[réf. nécessaire]. L'ensemble des méthodes mises en place ne concernent que des familles données d'équations différentielles, dont la spécificité se justifie au niveau de leur(s) application(s) respective(s).
Résolution par quadrature de certaines équations différentielles classiques
Équations scalaires d'ordre un, sous forme résolue Équation à variables séparées 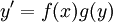
Soluble par primitivations et raccordements Équation linéaire d'ordre un 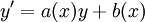
Soluble par changement de variable et primitivation Équation de Bernoulli 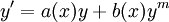
Se ramène à une équation linéaire par changement de variable Équation de Riccati 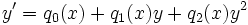
Soluble lorsqu'une solution particulière est connue (se ramène alors à une équation de Bernoulli par changement de variable) Équation homogène 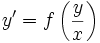
Se ramène à une équation à variables séparées par changement de variable Équations scalaires d'ordre un, sous forme non résolue Équation incomplète 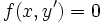 ou
ou 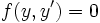
Soluble par paramétrage et primitivation Équation homogène non résolue 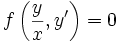
Se ramène par paramétrage à une équation à variables séparées Équation de Lagrange 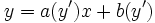
Soluble par changement de variable et raccordements Équation de Clairaut 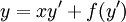
Cas particulier du précédent Équations scalaires d'ordre supérieur à un Équation linéaire à coefficients constants 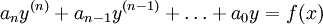
Ramené à la résolution d'un polynôme et à la méthode de variation des constantes Équation d'Euler 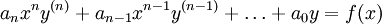
Se ramène par changement de variable au cas des coefficients constants Équation d'ordre deux 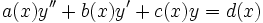
Soluble si on connaît une solution particulière de l'équation homogène ; raccordements Équations vectorielles Équation linéaire à coefficients constants 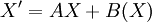
Ramené à un calcul d'exponentielle d'endomorphisme et à la méthode de variation des constantes Catégorie : Équation différentielle
Wikimedia Foundation. 2010.
