Regroupement hiérarchique

Dans le domaine informatique, et plus précisément dans le domaine de l'analyse et de la classification automatique de données, la notion de regroupement hiérarchique recouvre différentes méthodes de clustering, c'est-à-dire de classification par algorithme de classification.

La classification ascendante hiérarchique

C'est une méthode de classification automatique utilisée en analyse des données ; à partir d'un ensemble Ω de n individus, son but est de répartir ces individus dans un certain nombre de classes.

La méthode suppose qu'on dispose d'une mesure de dissimilarité entre les individus; dans le cas de points situés dans un espace euclidien, on peut utiliser la distance comme mesure de dissimilarité. La dissimilarité entre des individus x et y sera notée dissim(x,y).

La classification ascendante hiérarchique est dite ascendante car elle part d'une situation où tous les individus sont seuls dans une classe, puis sont rassemblés en classes de plus en plus grandes. Le qualificatif "hiérarchique" vient du fait qu'elle produit une hiérarchie H, l'ensemble des classes à toutes les étapes de l'algorithme, qui vérifie les propriétés suivantes:

• : au sommet de la hiérarchie, lors qu'on groupe de manière à obtenir une seule classe, tous les individus sont regroupés
• : en bas de la hiérarchie, tous les individus se trouvent seuls
• ou ou

Algorithme

Principe

Initialement, chaque individu forme une classe, soit n classes. On cherche à réduire le nombre de classes à nb_classes < n, ceci se fait itérativement. A chaque étape, on fusionne deux classes, réduisant ainsi le nombre de classes. Les deux classes choisies pour être fusionnées sont celles qui sont les plus "proches", en d'autres termes, celles dont la dissimilarité entre elles est minimale, cette valeur de dissimilarité est appelée indice d'agrégation. Comme on rassemble d'abord les individus les plus proches, la première itération a un indice d'agrégation faible, mais celui-ci va croître d'itération en itération.

Mesure de dissimilarité inter-classe

La dissimilarité de deux classes C₁ = x,C₂ = y contenant chacune un individu se définit simplement par la dissimilarité entre ces individus. dissim(C₁,C₂) = dissim(x,y)

Lorsque les classes ont plusieurs individus, il existe de multiples critères qui permettent de calculer la dissimilarité. Les plus simples sont les suivants:

• Le saut minimum retient le minimum des distances entre individus de C₁ et C₂:
• Le saut maximum est la dissimilarité entre les individus de C₁ et C₂ les plus éloignés:
• Le lien moyen consiste à calculer la moyenne des distances entre les individus de C₁ et C₂:
• La distance de Ward vise à maximiser l'inertie inter-classe: avec n₁ et n₂ les effectifs des deux classes, G₁ et G₂ leurs centres de gravité respectifs

Implémentation en pseudo-code

Entrées:

• individus: liste d'individus
• nbClasses: nombre de classes qu'on veut obtenir au final

Sortie:

• classes: liste de classes initialement vide, une classe est vue comme une liste d'individus

Pour i=1 à individus.longueur Faire
    classes.ajouter(nouvelle classe(individu[i]));
Fin Pour
Tant Que classes.longueur > nbClasses Faire
    // Calcul des dissimilarités entre classes dans une matrice triangulaire supérieure
    matDissim = nouvelle matrice(classes.longueur,classes.longueur);
    Pour i=1 à classes.longueur Faire
        Pour j=i+1 à classes.longueur Faire
            matDissim[i][j] = dissim(classes[i],classes[j]);
       Fin Pour
    Fin Pour
    // Recherche du minimum des dissimilarités
    Soit (i,j) tel que matDissim[i][j] = min(matDissim[k][l]) avec 1<=k<=classes.longueur et k+1<=l<=classes.longueur;
    // Fusion de classes[i] et classes[j]
    Pour tout element dans classes[j] Faire
        classes[i].ajouter(element);
    Fin pour
    supprimer(classes[j]);
Fin Tant Que

Dendrogramme

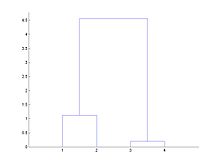
Exemple de dendrogramme

Un dendrogramme est la représentation graphique d'une classification ascendante hiérarchique ; Il se présente souvent comme un arbre binaire dont les feuilles sont les individus alignés sur l'axe des abscisses. Lors que deux classes ou deux individus se rejoignent avec l'indice d'agrégation τ, des traits verticaux sont dessinés de l'abscisse des deux classes jusqu'à l'ordonnée τ, puis ils sont reliés par un segment horizontal. À partir d'un indice d'agrégation τ, on peut tracer une droite d'ordonnée τ qui permet de voir une classification sur le dendrogramme.
Des versions plus complexes d'arbre de classification peuvent éventuellement aider à construire un arbre de décision.

Logiciels

• Alceste (logiciel)  ; logiciel de classification descendante ;
• IMSL ; bibliothèque mathématique et statistique

Voir aussi

Articles connexes

Liens externes

• A visual expedition inside the Linux file systems: étude des similarités entre les systèmes de fichiers implémentés dans Linux, et exemple de classification ascendante hiérarchique

Bibliographie

• Thèse « Contextualisation, visualisation et évaluation en apprentissage non supervisé » de Laurent Candillier (Université de Lille 3), 2006/09/15, PDF, 250 pages.

Notes et références

• Portail des probabilités et des statistiques
• Portail de l’informatique