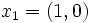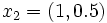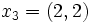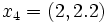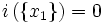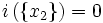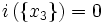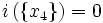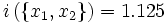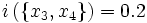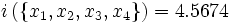Hierarchie (mathematiques)

Hierarchie (mathematiques): Hiérarchie (mathématiques)

On considère un ensemble 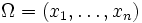$\Omega=(x_1,\dots,x_n)$ d'individus et un ensemble 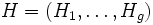$H=(H_1,\dots,H_g)$ de parties de $Ω$ . H est une hiérarchie sur $Ω$ si et seulement si :

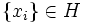quel que soit i, $\{x_i\}\in H$ .

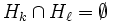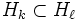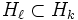quels que soient k et $\ell$ , $H_k\cap H_\ell=\emptyset$ ou $H_k\subset H_\ell$ ou $H_\ell\subset H_k$ .

Par exemple, pour un ensemble $Ω = (x 1, x 2, x 3, x 4)$ l'ensemble

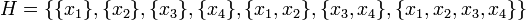
$H=\left\{\{x_1\},\{x_2\},\{x_3\},\{x_4\},\{x_1,x_2\},\{x_3,x_4\},\{x_1,x_2,x_3,x_4\}\right\}$

est une hiérarchie.

Indice sur une hiérarchie

On appelle indice sur un hiérarchie H de $Ω$ une fonction i de $H$ dans 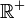$\mathbb{R}^+$ vérifiant les propriétés :

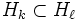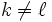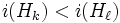si $H_k\subset H_\ell$ et $k\neq\ell$ , alors, $i(H_k)<i(H_\ell)$ .

quel que soit $x i$ de $Ω$ , $i ({x i}) = 0$ .

Le couple $(H, i)$ est alors appelé hiérarchie indicée.

Dans le cas de données continues, la fonction d'inertie définit un indice. En considérant l'exemple précédent et en considérant que les points $x i$ sont des points de 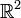$\mathbb{R}^2$ de coordonnées

$x_1=(1,0)\,$

$x_2=(1,0.5)\,$

$x_3=(2,2)\,$

$x_4=(2,2.2)\,$

La fonction d'inertie prend les valeurs suivantes :

$i\left(\{x_1\}\right)=0\,$

$i\left(\{x_2\}\right)=0\,$

$i\left(\{x_3\}\right)=0\,$

$i\left(\{x_4\}\right)=0\,$

$i\left(\{x_1,x_2\}\right)=1.125\,$

$i\left(\{x_3,x_4\}\right)=0.2\,$

$i\left(\{x_1,x_2,x_3,x_4\}\right)=4.5674\,$

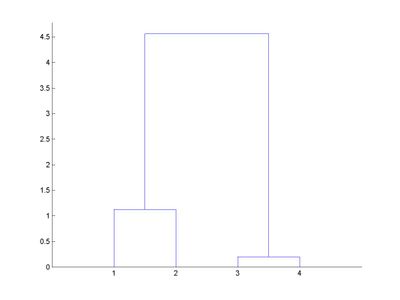
Une telle hiérarchie peut être représentée par le dendrogramme suivant :

Portail des mathématiques

Ce document provient de « Hi%C3%A9rarchie (math%C3%A9matiques) ».

Catégorie : Théorie des ordres

Contenu soumis à la licence CC-BY-SA. Source : Article Hierarchie (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Hiérarchie (mathématiques) — On considère un ensemble d individus et un ensemble de parties de Ω. H est une hiérarchie sur Ω si et seulement si : . quel que soit i, . . quels que soient k et … Wikipédia en Français
MATHÉMATIQUES , DE LA DIVERSITÉ À L’UNIFICATION — «Ce que nous appelons la réalité objective, c’est, en dernière analyse, ce qui est commun à plusieurs êtres pensants, et pourrait être commun à tous; cette partie commune [...], ce ne peut être que l’harmonie exprimée par des lois mathématiques.» … Encyclopédie Universelle
MATHÉMATIQUES (FONDEMENTS DES) — Au sens premier et fort, le mot «fondement» désigne la base, jugée inébranlable, sur laquelle repose un corps d’énoncés, un système de connaissances, un complexe de croyances ou de conduites. «Reposer sur la base» signifie ici «trouver en elle à… … Encyclopédie Universelle
Hierarchie de Borel — Hiérarchie de Borel Définition des ensembles de Borel Une algèbre sur un ensemble X est une collection de sous ensembles de X vérifiant les conditions suivantes: Si , alors Toute union finie d … Wikipédia en Français
Hiérarchie De Borel — Définition des ensembles de Borel Une algèbre sur un ensemble X est une collection de sous ensembles de X vérifiant les conditions suivantes: Si , alors Toute union finie d … Wikipédia en Français
Hiérarchie de borel — Définition des ensembles de Borel Une algèbre sur un ensemble X est une collection de sous ensembles de X vérifiant les conditions suivantes: Si , alors Toute union finie d … Wikipédia en Français
Hiérarchie de croissance rapide — En théorie de la calculabilité et en théorie de la démonstration, une hiérarchie de croissance rapide (parfois appelée une hiérarchie de Grzegorczyk (en) étendue) est une famille, indexée par les ordinaux, de fonctions rapidement croissantes … Wikipédia en Français
Hiérarchie de Borel — La hiérarchie de Borel désigne une description de la tribu des boréliens d un espace topologique X comme une réunion croissante d ensembles de parties de X, indexée par le premier ordinal non dénombrable. Sommaire 1 Notations préliminaires 2… … Wikipédia en Français
Hiérarchie polynomiale — Représentation graphique de la hiérarchie polynomiale. Les flèches indiquent l inclusion. En théorie de la complexité, la hiérarchie polynomiale est une hiérarchie de classes de complexité qui étend la notion de classes P, NP, co NP. Définition… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts