Processus d'Ornstein-Uhlenbeck

Processus d'Ornstein-Uhlenbeck

En mathématiques, le processus d'Ornstein-Uhlenbeck, nommé après Leonard Ornstein (en) et George Uhlenbeck et aussi connu sous le nom de mean-reverting process, est un processus stochastique décrit par l'équation différentielle stochastique

dr_t = -\theta (r_t-\mu)\,dt + \sigma\, dW_t,\,

où θ, μ et σ sont des paramètres déterministes et Wt est le processus de Wiener.

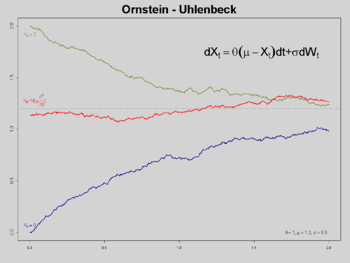Trois exemples du processus d'Ornstein-Uhlenbeck avec θ=1, μ=1.2, σ=0.3:
Bleu : Valeur initiale a=0 (p. s.)
Vert : Valeur initiale a=2 (p. s.)
Rouge : Valeur initiale distribuée normalement ainsi le procédé a une mesure invariante

Solution

Cette équation est résolue par la méthode de variation des constantes. Appliquons le lemme d'Itō à la fonction f(rt,t) = rteθt pour obtenir

df(r_t,t) = \theta r_t e^{\theta t}\, dt + e^{\theta t}\, dr_t\,
= e^{\theta t}\theta \mu \, dt + \sigma e^{\theta t}\, dW_t. \,

En intégrant de 0 à t, on obtient

r_t e^{\theta t} = r_0 + \int_0^t e^{\theta s}\theta \mu \, ds + \int_0^t \sigma e^{\theta s}\, dW_s \,

d'où nous voyons

r_t = r_0 e^{-\theta t} + \mu(1-e^{-\theta t}) + \int_0^t \sigma e^{\theta (s-t)}\, dW_s. \,

Ainsi, le premier moment est donné (en supposant que r0 est une constante) par :

E(rt) = r0e − θt + μ(1 − e − θt).

s \wedge t = \min(s,t) On peut utiliser l'isométrie d'Itō (en) pour calculer la covariance

\operatorname{cov}(r_s,r_t)= E[(r_s - E[r_s])(r_t - E[r_t])]
= E[\int_0^s \sigma e^{\theta (u-s)}\, dW_u \int_0^t \sigma e^{\theta (v-t)}\, dW_v ]
= \sigma^2 e^{-\theta (s+t)}E[\int_0^s e^{\theta u}\, dW_u \int_0^t e^{\theta v}\, dW_v ]
= \frac{\sigma^2}{2\theta} \, e^{-\theta (s+t)}(e^{2\theta (s \wedge t)}-1).\,

Il est aussi possible (et souvent commode) de représenter rt (sans condition) en tant que mesure transformée du temps du processus Wiener :

r_t=\mu+{\sigma\over\sqrt{2\theta}}W(e^{2\theta t})e^{-\theta t}

ou avec condition (r0 donné) comme

r_t=r_0 e^{-\theta t} +\mu (1-e^{-\theta t})+ {\sigma\over\sqrt{2\theta}}W(e^{2\theta t}-1)e^{-\theta t}.

Le processus d'Ornstein-Uhlenbeck (un exemple de processus gaussien à variance bornée) admet une distribution de probabilité stationnaire, contrairement au processus de Wiener.

L'intégrale temps de ce processus peut être utilisée pour générer un bruit avec un spectre de puissance 1/f.

Application

Le modèle de Vasicek (en) des taux d'intérêt est un exemple de processus d'Ornstein-Uhlenbeck.



Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Processus d'Ornstein-Uhlenbeck de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Ornstein-Uhlenbeck — Modèle OUV Finance Modèle OUV (Ornstein, Uhlenbeck, Vasicek) est utilisé pour calculer les options sur taux. Mathématique Nommé après Leonard Salomon Ornstein et George Eugene Uhlenbeck et qui est aussi connu sous le nom de mean reverting process …   Wikipédia en Français

  • Modèle OUV (Ornstein, Uhlenbeck, Vasicek) — Modèle OUV Finance Modèle OUV (Ornstein, Uhlenbeck, Vasicek) est utilisé pour calculer les options sur taux. Mathématique Nommé après Leonard Salomon Ornstein et George Eugene Uhlenbeck et qui est aussi connu sous le nom de mean reverting process …   Wikipédia en Français

  • Processus CIR — Le processus CIR (d après ses créateurs John C. Cox, Jonathan E. Ingersoll, et Stephen A. Ross) est un processus stochastique défini par l équation différentielle stochastique suivante: où θ et σ sont des paramètres positifs. Il peut être défini… …   Wikipédia en Français

  • Modele OUV — Modèle OUV Finance Modèle OUV (Ornstein, Uhlenbeck, Vasicek) est utilisé pour calculer les options sur taux. Mathématique Nommé après Leonard Salomon Ornstein et George Eugene Uhlenbeck et qui est aussi connu sous le nom de mean reverting process …   Wikipédia en Français

  • Modèle OUV — Finance Modèle OUV (Ornstein, Uhlenbeck, Vasicek) est utilisé pour calculer les options sur taux. Mathématique Nommé après Leonard Salomon Ornstein et George Eugene Uhlenbeck et qui est aussi connu sous le nom de mean reverting process, le… …   Wikipédia en Français

  • OUV — Modèle OUV Finance Modèle OUV (Ornstein, Uhlenbeck, Vasicek) est utilisé pour calculer les options sur taux. Mathématique Nommé après Leonard Salomon Ornstein et George Eugene Uhlenbeck et qui est aussi connu sous le nom de mean reverting process …   Wikipédia en Français

  • Calcul stochastique — Le calcul stochastique est l’étude des phénomènes aléatoires dépendant du temps. À ce titre, il est une extension de la théorie des probabilités. Sommaire 1 Applications 2 Processus aléatoires 3 Filtrations …   Wikipédia en Français

  • Calcul Stochastique — Le calcul stochastique est l’étude des phénomènes aléatoires dépendant du temps. À ce titre, il est une extension de la théorie des probabilités. Sommaire 1 Applications 2 Processus aléatoires 3 Filtrations …   Wikipédia en Français

  • Calcul sto — Calcul stochastique Le calcul stochastique est l’étude des phénomènes aléatoires dépendant du temps. À ce titre, il est une extension de la théorie des probabilités. Sommaire 1 Applications 2 Processus aléatoires 3 Filtrations …   Wikipédia en Français

  • Mouvement brownien — d une particule. Le mouvement brownien, ou processus de Wiener, est une description mathématique du mouvement aléatoire d une « grosse » particule immergée dans un fluide et qui n est soumise à aucune autre interaction que des chocs… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”