Calcul sto

Le calcul stochastique est l’étude des phénomènes aléatoires dépendant du temps. À ce titre, il est une extension de la théorie des probabilités.

Sommaire 1 Applications 2 Processus aléatoires 3 Filtrations 3.1 Espérance conditionnelle selon une filtration 4 Processus d'Itō 4.1 Intégrale d'Itô 4.2 Définition d'un processus d'Itô 5 Autre prescription 6 Processus usuels 7 Martingales exponentielles 8 Intégrale de Wiener et intégrale stochastique 8.1 Lemme d’Itô 9 Equations différentielles stochastiques 10 Processus d’Ornstein-Uhlenbeck 11 Problèmes de contrôle optimal 12 Méthodes de simulation 12.1 Méthode de Monte-Carlo 12.2 Simulation par arbres recombinants 13 Articles connexes 14 Bibliographie 15 Notes

Applications

Le domaine d’application du calcul stochastique comprend :

• la mécanique quantique,
• le traitement du signal,
• la chimie,
• les mathématiques financières,
• la météorologie,
• et même la musique.

Processus aléatoires

Un processus aléatoire X est une famille de variables aléatoires indexée par un sous-ensemble de ou 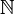, souvent assimilé au temps (voir aussi Processus stochastique). C'est donc une fonction de deux variables : le temps et l'état du monde ω. L'ensemble des états du monde est traditionnellement noté Ω. L'application qui à un ω fixé associe X(ω,t) , t variable, est appelée trajectoire du processus; c'est une simple fonction du temps (sans caractère aléatoire) qui représente la réalisation particulière du processus sous l'occurence ω. Pour un t donné , X(ω,t) est une simple variable aléatoire dont la valeur exacte n'est connue qu'en t. Le mouvement brownien est un exemple particulièrement simple de processus aléatoire indexé par . Il peut être défini comme l'unique processus W_t à accroissement gaussien tel que la corrélation entre W_t et W_s soit min(t,s). On peut également le voir comme la limite d'une marche aléatoire lorsque le pas de temps tend vers 0.

Filtrations

Une filtration F_t, 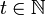est une famille de sous-tribus emboîtées de Ω, qui peut s’interpréter comme l’information disponible qui évolue au cours du temps. Ainsi, une filtration est une famille de sigma-algèbres, indexée par le temps 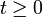telle que 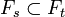si 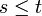, ce qui reflète l'augmentation de l'information disponible.

Espérance conditionnelle selon une filtration

Processus d'Itō

Le processus d'Itō, d'après le nom de son inventeur Kiyoshi Itō, traite des opérations mathématiques dans un processus stochastique. Le plus important est l'intégrale stochastique d'Itō.

Intégrale d'Itô

Avant le calcul, indiquons que :

• Les majuscules telles que X notent les variables aléatoires.
• Les majuscules avec en indice un t (par exemple B_t) notent un processus stochastique qui est une famille de variables aléatoires indexée par t.
• Un petit d à gauche d'un processus (par exemple dB_t) signifie un changement infinitésimal dans le processus aléatoire qui est une variable aléatoire.

L'intégrale stochastique d'un processus X_t par rapport à un processus B_t est décrite par l'intégrale :

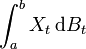
et est définie comme la limite en moyenne quadratique des sommes correspondantes de la forme :

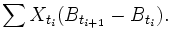
Un point essentiel lié à cette intégrale est le lemme d'Itô.

La somme comme le produit de variables aléatoires est définie dans la théorie des probabilités. La somme implique une convolution de la fonction de densité des probabilités, et la multiplication est une addition répétée.

Définition d'un processus d'Itô

Une fois précisée la définition choisie pour une intégrale stochastique, on définit alors un processus d'Itô comme étant une processus stochastique X_t de la forme

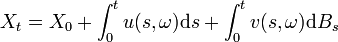
avec u et v deux fonctions aléatoires satisfaisant quelques hypothèses techniques d'adaptation au processus B_t et ω est une réalisation dans l'espace de probabilité sous-jacent.

Dans le formalisme du calcul différentiel avec la prescription d'Itô on note de façon équivalente la relation précédente comme

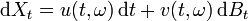
Autre prescription

Il existe une autre prescription notable pour définir une intégrale stochastique, c'est la prescription de Stratonovich. L'intégrale de Stratonovich est définie comme la limite des sommes discrètes

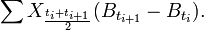
La différence notable avec la prescription d'Itô est que la quantité 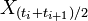n'est pas indépendante au sens des probabilités de la variable 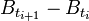. Ainsi, contrairement à la prescription d'Ito, dans la prescription de Stratonovich on a

ce qui complique, de ce point de vue, certains calculs. Cependant l'utilisation de la prescription de Stratonovich ne choisit pas une direction du temps privilégiée contrairement à celle d'Itô ce qui implique que les processus stochastiques définis par l'intégrale de Stratonovich satisfont des équations différentielles stochastiques invariantes par renversement du temps. Pour cette raison, cette prescription est souvent utilisée en physique statistique.

Il faut noter cependant qu'il est possible de passer de l'une à l'autre des prescriptions en effectuant des changements de variables simples ce qui les rend équivalentes. Le choix de prescription est donc une question de convenance.

Processus usuels

Martingales exponentielles

Intégrale de Wiener et intégrale stochastique

Soit Z le mouvement brownien standard défini sur l’espace probabilisé (Ω,A,F,P) et σ un processus adapté à F. On suppose par ailleurs que σ vérifie :

.

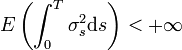Alors, l’intégrale stochastique de σ par rapport à Z est la variable aléatoire :

.

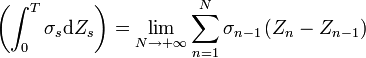Lemme d’Itô

Soit x un processus stochastique tel qu'on ait dx = adt + bdz où z est un processus de Wiener standard.

Alors d'après le lemme d'Itô, on a pour une fonction G = G(x,t)

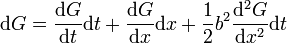
Equations différentielles stochastiques

Une équation différentielle stochastique (EDS) est la donnée d’une équation du type dX = μ(X,t)dt + σ(X,t)dW_t, où X est un processus aléatoire inconnu, que l’on appelle communément équation de diffusion. Intégrer l’EDS, c’est trouver l’ensemble des processus vérifiant la diffusion entiere.

Processus d’Ornstein-Uhlenbeck

Le processus d'Ornstein-Uhlenbeck est un processus stochastique décrivant (entre autres) la vitesse d'une particule dans un fluide, en dimension 1.

On le définit comme étant la solution X_t de l'équation différentielle stochastique suivante :

,

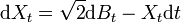où B_t est un mouvement brownien standard, et avec X₀ une variable aléatoire donnée. Le terme dB_t traduit les nombreux chocs aléatoires subis par la particule, alors que le terme − X_tdt représente la force de frottement subie par la particule.

La formule d'Itô appliquée au processus e^tX_t nous donne :

,

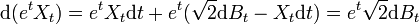soit, sous forme intégrale :

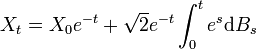
Par exemple, si X₀ vaut presque sûrement x, la loi de X_t est une loi gaussienne de moyenne xe ^{− t} et de variance 1 − e ^{− 2t}, ce qui converge en loi quand t tend vers l'infini vers la loi gaussienne centrée réduite.

Problèmes de contrôle optimal

Méthodes de simulation

Méthode de Monte-Carlo

Les méthodes de Monte-Carlo reposent sur la Loi des grands nombres : en répétant un grand nombre de fois une expérience, de façon (théoriquement) indépendante, on obtient une approximation de plus en plus fiable de la vraie valeur de l'espérance du phénomène observé.

De telles méthodes sont notamment utilisées en finance pour la valorisation d’options pour lesquelles il n’existe pas de formule fermée, mais uniquement des approximations numériques.

Simulation par arbres recombinants

Articles connexes

• Chaîne de Markov
• Modèle de Markov caché
• Processus de décision markovien
• Mouvement brownien
• Physique statistique
• Modèle des urnes d'Ehrenfest
• Processus stochastique
• Équation différentielle stochastique
• Matrice stochastique
• Calculateur stochastique

Bibliographie

• Nathalie Bartoli et Pierre Del Moral, Simulation & algorithmes stochastiques, Cépaduès, 2001 (ISBN 2-85428-560-3)
• Mario Lefebvre, Processus stochastiques appliqués, Hermann, 2006 (ISBN 2-7056-6561-7)
• Nathalie Bartoli et Pierre Del Moral, Calcul stochastique et modèles de diffusions, Dunod, 2006 (ISBN 2-10-050135-6)
• Bassel Solaiman, Processus stochastiques pour l'ingénieur, Presses Polytechniques et Universitaires Romandes, 2006 (ISBN 2-88074-668-X)

Notes

• Portail des probabilités et des statistiques