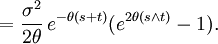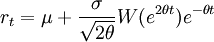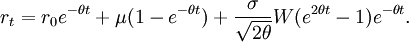- Ornstein-Uhlenbeck
-
Modèle OUV
Finance
Modèle OUV (Ornstein, Uhlenbeck, Vasicek) est utilisé pour calculer les options sur taux.
Mathématique
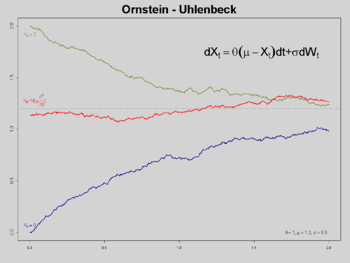
Nommé après Leonard Salomon Ornstein et George Eugene Uhlenbeck et qui est aussi connu sous le nom de mean-reverting process, le processus r est un processus d'Ornstein-Uhlenbeck (OU), si son équation différentielle stochastique (EDS) est de la forme:
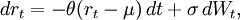
où θ, μ et σ sont des paramètres déterministes et Wt suivant la loi de Wiener.
Solution
Cette équation est résolue par variation de paramètres. Appliquons le lemme d'Itō à la fonction f(rt,t) = rteθt pour obtenir
En intégrant de 0 à t, on obtient
d'où nous voyons
Ainsi, le premier moment (mathématique) est donné par (en supposant que r0 est une constante),
- E(rt) = r0e − θt + μ(1 − e − θt).
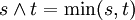 On peut utiliser l'isométrie d'Itō pour calculer la covariance
On peut utiliser l'isométrie d'Itō pour calculer la covarianceC'est aussi possible (et souvent commode) de représenter rt (sans réserve) en tant que mesure transformée du temps du processus Wiener :
ou condition (donné r0) comme
Le processus d'Ornstein-Uhlenbeck (un exemple de processus Gaussien à variance liée) admet un procédé stationnaire à distribution probable, en opposition au processus de Wiener.
L'intégrale Temps du procédé peut être utilisée pour générer du bruit avec a 1/f pouvoir spectrum.- Portail des mathématiques
Catégories : Processus stochastique | Équation différentielle
Wikimedia Foundation. 2010.

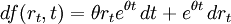
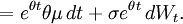
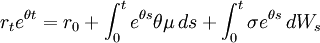
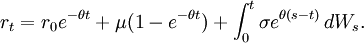
![\operatorname{cov}(r_s,r_t)= E[(r_s - E[r_s])(r_t - E[r_t])]](/pictures/frwiki/52/4237c825a19af9dfca73e225d32a3b8a.png)
![= E[\int_0^s \sigma e^{\theta (u-s)}\, dW_u \int_0^t \sigma e^{\theta (v-t)}\, dW_v ]](/pictures/frwiki/54/62201b52a097081715fb67f5ef08f468.png)
![= \sigma^2 e^{-\theta (s+t)}E[\int_0^s e^{\theta u}\, dW_u \int_0^t e^{\theta v}\, dW_v ]](/pictures/frwiki/54/609af4da9bea227a1290e9c252c1838c.png)