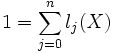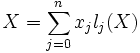Polynômes de Lagrange

Polynômes de Lagrange

Interpolation lagrangienne

En analyse numérique, les polynômes de Lagrange, du nom de Joseph Louis Lagrange, permettent d'interpoler une série de points par un polynôme qui passe exactement par ces points appelés aussi nœuds. Cette technique d'interpolation polynomiale a été découverte par Edward Waring en 1779 et redécouverte plus tard par Leonhard Euler en 1783.

Sommaire

Définition

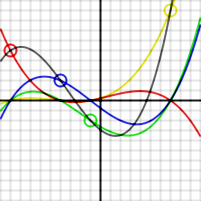Cette image montre, pour 4 points ((-9, 5), (-4, 2), (-1, -2), (7, 9)), l'interpolation polynomiale L(x) (de degré 3), qui est la somme des polynômes de base y0.l0(x), y1.l1(x), y2.l2(x) et y3.l3(x). Le polynôme d'interpolation passe par les 4 points de contrôle, et chaque polynôme de base passe par son point de contrôle respectif et vaut 0 pour les x correspondant aux autres points de contrôle.

On se donne n + 1 points 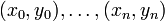(x_0, y_0),\dots,(x_n, y_n) (avec les xi distincts 2 à 2). On se propose de construire un polynôme de degré minimal qui en les abscisses 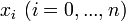x_i\ (i=0,...,n) prend les valeurs yi, ce qui est achevé par la méthode suivante.

Polynômes de Lagrange

Les polynômes de Lagrange associés à ces points sont les polynômes définis par :

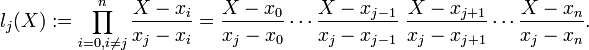
l_j(X) := \prod_{i=0, i\neq j}^{n} \frac{X-x_i}{x_j-x_i} = \frac{X-x_0}{x_j-x_0} \cdots \frac{X-x_{j-1}}{x_j-x_{j-1}} ~ \frac{X-x_{j+1}}{x_j-x_{j+1}} \cdots \frac{X-x_{n}}{x_j-x_{n}}.

On a en particulier deux propriétés :

  1. lj est de degré n pour tout j
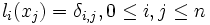  2. l_i(x_j) = \delta_{i,j}, 0 \leq i,j \leq n c'est-à-dire li(xi) = 1 et li(xj) = 0 pour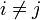 i\ne j

Polynôme d'interpolation

Le polynôme défini par 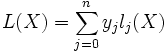L(X) = \sum_{j=0}^{n} y_j l_j(X) est l'unique polynôme de degré au plus n vérifiant L(xi) = yi pour tout i.

En effet 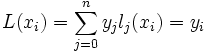L(x_i) = \sum_{j=0}^{n} y_j l_j(x_i)=y_i et L est une combinaison linéaire de polynômes de degré au plus n donc est de degré n au plus.

Si un autre polynôme, Q, vérifie ces propriétés alors L − Q est de degré n au plus, et s'annule en n + 1 points (les xk) donc est nul ce qui prouve l'unicité.

Autre écriture

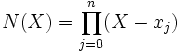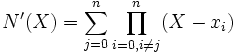Posons N(X)=\prod^{n}_{j=0}(X-x_j). On a N(xi) = 0 et, en utilisant la formule de Leibniz N'(X)=\sum^{n}_{j=0}\prod^{n}_{i=0,i\ne j}(X-x_i).

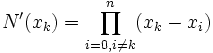En particulier, comme tous les produits sont nuls en xk sauf un  : N'(x_k)=\prod^{n}_{i=0,i\ne k}(x_k-x_i).

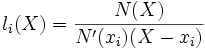
Ainsi l_i(X)={N(X) \over N'(x_i)(X-x_i)}

On peut utiliser N pour traduire l'unicité : si Q vérifie Q(xi) = yi pour tout i alors Q − L s'annule aux points xi donc est un multiple de N. Il est donc de la forme Q(X) = L(X) + N(X).P(X) où P est un polynôme quelconque.

Base de polynômes

On se donne n + 1 scalaires distincts 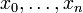x_0,\ldots,x_n. Pour tout polynôme P appartenant à Kn[X], si on pose yi = P(xi), P est le polynôme d'interpolation correspondant aux points : il est égal au polynôme L défini ci-dessus.

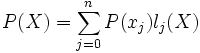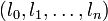On a donc P(X)=\sum_{j=0}^{n} P(x_j) l_j(X) donc (l_0,l_1,\dots,l_n) forme une famille génératrice de Kn[X]. Comme son cardinal (égal à n + 1) est égal à la dimension de l'espace, elle en est une base.

Exemples : en choisissant P = 1 ou P = X on a

  1. 1=\sum_{j=0}^{n} l_j(X)
  2. X=\sum_{j=0}^{n} x_jl_j(X)

En fait c'est la base dont la base duale est la famille des n + 1 formes linéaires ui de Dirac définies par ui(P) = P(xi).

Applications

  1. Ils peuvent être utilisés pour calculer la matrice inverse d'une matrice de Vandermonde
  2. Ils interviennent dans la démonstration du critère de diagonalisabilité par les polynômes annulateurs.

Idée principale

Résoudre un problème d'interpolation conduit à inverser une matrice pleine de type matrice de Vandermonde. C'est un calcul lourd en nombre d'opérations. Les polynômes de Lagrange définissent une nouvelle base de polynômes qui permet de ne plus avoir une matrice pleine mais une matrice diagonale. Or, inverser une matrice diagonale est une opération instantanée.

Voir aussi

Liens internes

Lien externe

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Interpolation lagrangienne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polynômes de Lagrange de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Polynomes de Lagrange — Interpolation lagrangienne En analyse numérique, les polynômes de Lagrange, du nom de Joseph Louis Lagrange, permettent d interpoler une série de points par un polynôme qui passe exactement par ces points appelés aussi nœuds. Cette technique d… …   Wikipédia en Français

  • POLYNÔMES — La théorie des équations et des polynômes a été le propos essentiel de l’algèbre jusqu’au XIXe siècle (cf. ÉQUATIONS ALGÉBRIQUES, ALGÈBRE) et est à la base de la théorie des corps et de la théorie des nombres algébriques. Nous nous sommes limités …   Encyclopédie Universelle

  • Polynômes de Chebyshev — Polynôme de Tchebychev Les polynômes de Tchebychev sont nommés d après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) Tn d indice n = 0,1,2,...… …   Wikipédia en Français

  • Polynômes de Tchebychev — Polynôme de Tchebychev Les polynômes de Tchebychev sont nommés d après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) Tn d indice n = 0,1,2,...… …   Wikipédia en Français

  • Polynômes de Tchebytchev — Polynôme de Tchebychev Les polynômes de Tchebychev sont nommés d après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) Tn d indice n = 0,1,2,...… …   Wikipédia en Français

  • Polynômes d'Hermite — Polynôme d Hermite En mathématiques, les polynômes d Hermite sont une suite de polynômes qui a été nommée ainsi en l honneur de Charles Hermite (bien qu ils aient été surtout étudiés par Joseph Louis Lagrange lors de ses travaux sur les… …   Wikipédia en Français

  • Interpolation de Lagrange — Interpolation lagrangienne En analyse numérique, les polynômes de Lagrange, du nom de Joseph Louis Lagrange, permettent d interpoler une série de points par un polynôme qui passe exactement par ces points appelés aussi nœuds. Cette technique d… …   Wikipédia en Français

  • Interpolation de lagrange — Interpolation lagrangienne En analyse numérique, les polynômes de Lagrange, du nom de Joseph Louis Lagrange, permettent d interpoler une série de points par un polynôme qui passe exactement par ces points appelés aussi nœuds. Cette technique d… …   Wikipédia en Français

  • Polynôme de Lagrange — Interpolation lagrangienne En analyse numérique, les polynômes de Lagrange, du nom de Joseph Louis Lagrange, permettent d interpoler une série de points par un polynôme qui passe exactement par ces points appelés aussi nœuds. Cette technique d… …   Wikipédia en Français

  • Theoreme de Lagrange sur les polynomes — Théorème de Lagrange sur les polynômes Pour les articles homonymes, voir Théorème de Lagrange. Il s agit d un résultat trouvé par le mathématicien franco italien Joseph Louis Lagrange concernant les polynômes. Soit P un polynôme tel que: où les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”