Plans projectifs

La géométrie projective a permis de simplifier grandement des théorèmes de géométrie plane. La géométrie projective ne travaille que sur les alignements et les intersections, elle ignore angles et longueurs. Une telle démarche conduit à envisager des espaces différents de notre espace euclidien familier, à envisager même des structures anti-intuitives. On parle souvent du plan projectif comme s'il était unique mais c'est une erreur. Une autre manière d'étudier la géométrie projective consiste à progresser par ajouts successifs d'axiomes depuis une base minimaliste (des droites qui se coupent, des points reliés par une droite), les plans projectifs se diversifient. En résumé, le géomètre projectif travaille avec le crayon et la règle non-graduée, les autres géomètres utilisent aussi l'équerre, le té, le compas et la règle graduée.

Sommaire 1 Présentation des choix possibles 2 Cascade d'axiomes de plans projectifs 2.1 Plan projectif-tout-court 2.2 Plan projectif d'incidence (la base minimaliste) 2.2.1 Il y a peu de théorèmes dans un Plan Projectif d'Incidence 2.2.1.1 Combien de droites sur 1 point et dualité des axiomes 2.2.1.2 Un théorème intéressant est celui des 7 points 2.2.1.3 Quelques autodualités 2.2.1.4 Théorème du retournement 2.2.2 Concepts unificateurs 2.2.3 Figures harmoniques dans un PP d'incidence 2.2.3.1 Définition d'un quadruplet harmonique 2.2.3.2 Caractère désordonné d'un quadruplet harmonique 2.2.3.3 Les 2 autres quadruplets harmoniques de la figure. 2.2.3.4 Vocabulaire de l'harmonicité. 2.3 Plan projectif homogène (et barycentrique) 2.4 Plans projectifs fondamental, de Pappus, de Désargues, etc. 3 Transformations et configurations utiles 4 Cascade de théorèmes entre ces axiomes 5 des choix cornéliens pour approfondir les plans projectifs 6 Pour approfondir.

Présentation des choix possibles

Il existe plusieurs chemins pour aborder la géométrie projective. Une grande partie des difficultés tient au fait que nous sommes physiquement obligés de dessiner une figure d'un plan projectif sur le plan de la feuille de papier qui est située en réalité sur un plan métrique euclidien. Si on dessine un être mathématique imaginaire, parmi des milliers d'autres tout aussi imaginaires, sur une réalité physique unique on ne sait plus quelles propriétés concernent l'être issu de l'imagination et quelles propriétés concernent le plan métrique ordinaire, le contenu se confond avec le récipient. Et pourtant il faut bien expliquer cet être issu de l'imagination, y compris avec des petits dessins.

Au cours de l'histoire, plusieurs voies ont été utilisées.

• Les perspectivistes de la Renaissance traitaient le plan projectif comme un plan de l'espace ordinaire ayant telles et telles propriétés d'intersection ou d'alignement. Dans la même veine on définissait une conique comme l'intersection d'un cône de révolution avec un plan, le cône et le plan étant des éléments situés dans l'espace ordinaire, bien évidemment puisqu'on n'en connaissait pas d'autres.
• D'autres mathématiciens définissent le plan projectif comme une extension du plan affine.
• On peut aussi définir un plan projectif comme un plan qui possède un certain groupe de transformations qui laissent certaines choses invariantes, ces choses n'étant pas les distances ni les rapports ni les angles, mais les alignements et les birapports.
• Pour s'affranchir de la pénible ambiguïté du dessin de figures sur le plan du papier, autant trouver le moyen de raisonner sans aucune figure! C'est possible si on aborde le plan projectif d'une manière purement analytique, en partant d'un espace vectoriel de dimension 3 privé du vecteur nul, ensemble dont on prend l'ensemble-quotient relativement à une certaine relation d'équivalence. Ceci est très abstrait mais fonctionne très bien.
• Une variante de l'approche analytique est beaucoup plus concrète: les coordonnées homogènes, approche qui elle-même se subdivise en variantes
• Les coordonnées homogènes les plus faciles à manipuler sont celles qui partent des coordonnées cartésiennes (x,y) et leur rajoutent une troisième coordonnée Z qui est égale à 1 si le point est à distance finie, à 0 si le point est à l'infini. tout ceci reste très computationnel, esquive pour ainsi dire la véritable géométrie en réduisant tout à du calcul linéaire ou bilinéaire.
• Des coordonnées homogènes appelées coordonnées barycentriques peuvent être utilisées; elles ont le mérite de faire appel à une propriété géométrique concrète: le point (X,Y,Z) est le barycentre de trois points de base affectés des coefficients (X, Y, Z).

• En revanche, la démarche de présentation des plans projectifs que nous abordons ici répond à deux principes, 1) expliquer le maximum de concepts en termes de points et de droites qui se coupent, 2) construire les propriétés par l'emploi d'axiomes de plus en plus riches, y compris les propriétés des coniques. En matière de coniques d'ailleurs diverses démarches ont été suivies au cours de l'histoire, depuis la définition en termes d'intersection d'un cône et d'un plan jusqu'à la définition en termes de conservation d'un birapport.
• On peut opter pour la démarche de présentation des coniques qui consiste en une propriété d'alignement, celle de l'hexagramme de Pascal, figure particulièrement simple à comprendre sans grand bagage mathématique.

Cascade d'axiomes de plans projectifs

• « To construct a geometry is to state a system of axioms and to deduce all possible consequences from them. All systems of pure geometry ...are constructed in just this way. Their differences ...are differences not of principle or of method, but merely of richness of content and variety of application. » GH Hardy, extrait de , what is geometry? math. Gazette, 1925 , .

Plan projectif-tout-court

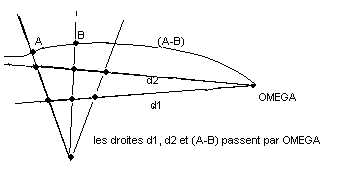
Un plan projectif (PP) est un ensemble de points et de droites (c'est-à-dire de groupements de points qu'on appellera droites). Un point est incident à cette droite s’il appartient à ce groupement. Une droite est incidente à un point si ce point fait partie de ce groupement. On dit aussi que cette droite passe par ce point ou que ce point est sur cette droite. Ce ne sont là que des questions de vocabulaire. Attention, une droite ne ressemble pas forcément aux bonnes vieilles droites de notre plan euclidien « naturel », ce n'est qu'un mot pour désigner des sous-ensembles de points. Une convention dans le dessin des figures, surtout lorsqu'elles dépassent le bord de page, est de « courber les droites ». Exemple :

C'est un exemple dans lequel pour certaines raisons les points A et B sont tels qu'apparemment leur droite (A-B) monte un peu trop, mais comme l'auteur veut exprimer que cette droite passe par OMEGA, il courbe cette droite sans aucun complexe. De même la droite m du plan de Fano ci-après ne peut être dessinée que courbée.

Plan projectif d'incidence (la base minimaliste)

Un plan projectif (PPI) d’incidence est un PP qui vérifie les axiomes :

1. Il existe au moins 2 points et une droite.
2. Chaque droite possède au moins 3 points.
3. Pour deux points distincts il existe une et une seule droite qui leur est incidente.
4. Deux droites distinctes ont un et un seul point commun.
5. Pour toute droite il existe au moins un point non incident à cette droite.

Il y a peu de théorèmes dans un Plan Projectif d'Incidence

Combien de droites sur 1 point et dualité des axiomes

Par tout point passent au moins 3 droites.

Démonstration. Soit le point M ; j'ai au moins 2 points M et N, donc une droite MN, qui contient au moins un troisième point P ; mais il existe au moins un point W hors de cette droite. Donc j'ai une droite WN qui ne passe pas par M ; cette droite contient un troisième point Z. Considérons la droite WNZ et le point extérieur M. Alors il existe 3 droites incidentes à M : MW, MN et MZ, qui sont toutes distinctes, sinon, par exemple, M, W et N seraient alignés sur WN qui contient aussi Z et est donc WNZ qui n'est pas incidente à M.

Un théorème intéressant est celui des 7 points

qui découle de nos maigres axiomes.

Tout PPI comporte au moins 7 points.

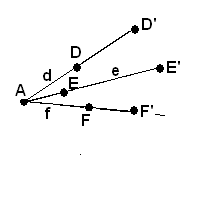
Démonstration: un PPI a au moins 1 point A. Par ce point A passent au moins 3 droites d e f; qui contiennent chacune au moins 2 autres points, à savoir D D' E E' F F', CQFD, il y a bien au moins 7 points. Une démonstration identique montre qu'il y a au moins 7 droites.

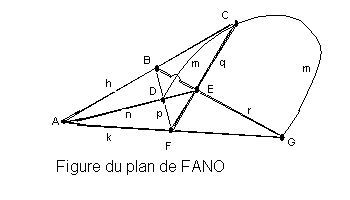
Remarque: Le plus petit plan d’incidence est le plan mnémotechnique de l'octonion de Fano : 7 points et 7 droites.

attention, (m) est la droite CDG, bien qu’elle n’ait pas l’allure d’une droite euclidienne ! m et r se coupent en l’unique point G, ce qui est signalé par le "petit pont" de BE sur DC. Chaque droite contient 3 points et chaque point est incident à trois droites.

On pourrait imaginer des PPI encore plus exotiques.

Quelques autodualités

On dit qu'une figure, une formule, un théorème est autodual s'il est conservé quand on échange les rôles des points et des droites. Quelques exemples.

• avec 2 éléments: l'incidence d'un point et d'une droite: le point A est incident à la droite d ⇔ la droite d est incidente au point A.
• 2 x2 éléments. Le rapport anharmonique de deux droites et 2 points.
• 3 x2 éléments. Le triangle et son trigone (ou tri-côté).
• 4, 5, 6 x2 éléments. Quelle figure?
• 7 x2 éléments. La figure de Fano.
• 8 x2 éléments. Quelle figure?
• 9 x2 éléments. Le théorème de Désargues
• 10 x2 éléments. Le théorème de Pappus.

Théorème du retournement

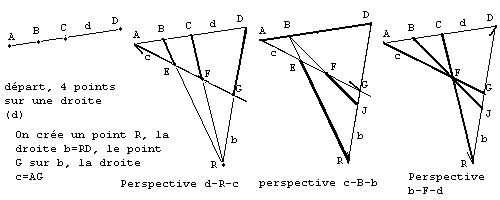
Enoncé: Étant donné un alignement ABCD, il existe une succession de perspectives unidimensionnelles qui le transforme en DCBA.

Démonstration: la séquence des perspectives donne

• sur d : A B C D
• centre R
• sur c : A E F G
• centre B
• sur b : D R J G
• centre F
• sur d : D C B A.

Concepts unificateurs

Pour y voir clair dans le foisonnement des axiomes et théorèmes géométriques, citons quelques grands concepts auxquels il est utile de se raccrocher:

• les figures dans l'espace: triangle, cercle, coniques....
• les transformations
• lois de composition internes des diverses transformations
• structure de certains groupes de transformations
• invariants d'une famille de transformations: "quels sont les invariants de telles transformations dans l'Espace?"
• structures d'Espace: "quelle est la structure d'Espace qui induit tel ou tel invariant de certaines transformations?"
• échafaudage axiomatique de diverses sortes d'Espaces

Figures harmoniques dans un PP d'incidence

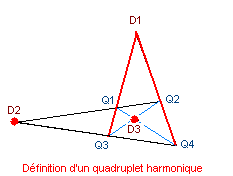
Définition d'un quadruplet harmonique

Un quadruplet est dit harmonique s'il est formé de deux droites (d1 et d2) et de deux points (D2 et D3) tels que: il existe un quadrangle complet Q1 Q2 Q3 Q4 dont D2 et D3 sont des points diagonaux et dont d1 et d2 sont les côtés qui passent par l'autre point diagonal(D1).

Sur cette figure le quadrangle complet est Q1 Q2 Q3 Q4, les 6 côtés sont Q1Q2 Q3Q4 Q1Q3 Q2Q4 Q1Q4 Q2Q3, ils engendrent les 3 points diagonaux D1 D2 D3, et le quadruplet {Q1Q3, Q2Q4, D2, D3} est harmonique.

Caractère désordonné d'un quadruplet harmonique

On remarquera que la figure d'incidence qui permet de définir le quadruplet harmonique {Q1Q3, Q2Q4, D2, D3} est la même que pour {Q1Q3, Q2Q4, D3, D2} ou {Q2Q4, Q1Q3, D2, D3} ou {Q2Q4, Q1Q3, D3, D2}. Ce qui signifie que cette notion est un quadruplet désordonné, l'essentiel étant de savoir qui sont les 2 droites et qui sont les 2 points

Les 2 autres quadruplets harmoniques de la figure.

si nous sommes munis uniquement des axiomes d'incidence, il n'y a qu'un théorème sur l'harmonicité: Lorsqu'un quadruplet est harmonique, alors deux autres le sont aussi. Ceci s'obtient simplement en choisissant un autre couple de points diagonaux dans le quadrangle complet. {Q1Q2, Q3Q4, D3, D1} et {Q1Q4, Q2Q3, D1, D2} sont aussi harmoniques.

Pour obtenir d'autres propriétés harmoniques le plan arguésien sera nécessaire.

Vocabulaire de l'harmonicité.

On parle d'un quadruplet harmonique formé de 2 droites et de 2 points, mais compte tenu du caractère désordonné du concept, on peut aussi bien parler d'un quadruplet harmonique formé d'une bidroite et d'un bipoint.

l'intersection des deux droites est appelée sommet du quadruplet, la droite qui joint les deux points est appelée axe du quadruplet.

En cas d'harmonie, on peut dire que D2 et D3 sont conjugués par rapport à la bidroite, ou que Q1Q3 et Q2Q4 sont sont conjuguées par rapport au bipoint.

On dit aussi que D2 est conjugué harmonique de D3 par rapport à la bidroite; ce qui est réciproque, D3 est conjugué harmonique de D2 par rapport à la bidroite.

Même vocabulaire pour les droites: Q2Q4 est conjuguée harmonique de Q1Q3 par rapport au bipoint.

On dit aussi que la droite D3D1 est la polaire du point D2 par rapport à la bidroite Q1Q3-Q2Q4, mais cette notion sera surtout utile dans l'étude des coniques.

On remarquera que la droite D3D1 est polaire de D2 simultanément par rapport à la bidroite Q1Q3-Q2Q4 et par rapport à la Q1Q4-Q2Q3, ce qui préfigure la polarité par rapport à toute conique passant par les 4 points Q1Q2Q3Q4.

Les géomètres euclidiens parlent de la division harmonique {D2,H,Q3,Q4} et du faisceau harmonique de droites {a,b,c,d}.

voir rapport anharmonique.

Plan projectif homogène (et barycentrique)

Le plan homogène est une création abstraite de géométrie analytique destinée à uniformiser les calculs d'intersections de droites sans se préoccuper de savoir si elles sont parallèles ou non. Dans un premier temps le plan homogène et les coordonnées homogènes ont un but simplement computationnel. Dans un deuxième temps si on approfondit les conséquences de la définition des coordonnées homogènes on s'aperçoit que ceci correspond à la définition d'un plan projectif; comme il existe plusieurs sortes de plans projectifs, on se demande duquel il s'agit et l'on peut démontrer que le plan projectif homogène répond au théorème fondamental de la géométrie projective.

Plans projectifs fondamental, de Pappus, de Désargues, etc.

La géométrie projective a permis de s'abstraire des impressions intuitives de la géométrie plane euclidienne. La géométrie projective ne travaille que sur les alignements et les intersections, elle ignore angles et longueurs. On part donc d'une base vraiment minimale à laquelle on ajoute des axiomes au compte-gouttes. Ainsi « tout univers possible dans l'imagination humaine » correspond à un ensemble d'axiomes qui définissent une structure d'Espace.

Les choses un peu compliquées commencent avec le théorème fondamental, les axiomes de Désargues et de Pappus, le théorème de Pascal ; tous ces concepts permettent de travailler sur des objets composites tels que les tripoints, tridroites, quadripoints, hexagrammes magiques pour aboutir à une théorie projective unifiée des coniques, théorie qui n'a pas besoin d'employer les notions de distance (point-point ou point-droite).

Transformations et configurations utiles

Cascade de théorèmes entre ces axiomes

des choix cornéliens pour approfondir les plans projectifs

Lorsque l’on aborde les plans projectifs selon une cascade d’axiomes reliés par une cascade de théorèmes il est possible d’hésiter, la tentation de tout démontrer d’un seul coup avec un théorème très puissant est forte, ou la tentation de tout démontrer algébriquement avec des formules de géométrie analytique.

Lorsque nous lisons actuellement des manuels de géométrie projective d'un formalisme absolu, sans figure, nous pensons que les étudiants ne peuvent, faute de formation adéquate, en comprendre la substance.-Anne Boyé, Pour la science n^o 21, novembre 2004-février 2005.

Pour approfondir.

• Axiomes de plans projectifs/homogènes
• Axiomes de plans projectifs/Suite des axiomes
• Traité projectif des coniques

Articles de Géométrie projective ou voisins à consulter.

[modifier]

Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes  • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques)

• Portail de la géométrie