Plan d'Argand-Cauchy

Plan d'Argand-Cauchy

Plan complexe

En mathématiques, le plan complexe (encore appelé plan de Cauchy ou plan d'Argand) désigne un plan dont chaque point est la représentation graphique d'un nombre complexe unique.

Définition

On associe en général le plan complexe à un repère 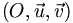(O, \vec{u}, \vec{v}) orthonormé direct. Dans un tel repère, tout point M est l'image d'un unique nombre complexe z qui est appelé affixe de cet unique point (dans ce cas, affixe est féminin : une affixe) : on note M(z).

Pour tout nombre complexe z tel que z = a + ib (où a et b sont des réels), on a la relation 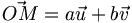\vec{OM} = a\vec{u} + b\vec{v}. On peut ainsi dire que la partie réelle de z est l'abscisse de M et que la partie imaginaire de z en est son ordonnée.

D'après cette égalité, tous les points de l'axe 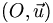(O, \vec{u}) sont tels que la partie imaginaire de leur affixe est nulle : leur affixe est donc un nombre réel. En conséquence, on appelle l'axe 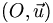(O, \vec{u}) axe des réels.

De la même façon, tous les points de l'axe 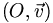(O, \vec{v}) sont tels que le partie réelle de leur affixe est nulle : leur affixe est donc un nombre imaginaire pur. En conséquence, on appelle l'axe 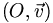(O, \vec{v}) axe des imaginaires.

(a,b) sont les coordonnées cartésiennes de z = a+ib dans le plan complexe. On peut aussi écrire z avec des coordonnées polaires (r,θ), ce qui correspond à l'écriture exponentielle z = r·exp(iθ). Dans ce cas, r est le module du nombre et θ est un de ses arguments (modulo 2π).

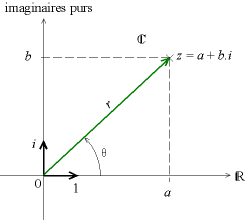
représentation graphique de z dans le plan complexe, coordonnées cartésiennes et polaire
Représentation graphique de z dans le plan complexe, coordonnées cartésiennes et polaire

Transformations du plan

La somme de deux vecteurs correspond à la somme de leurs affixes. Ainsi, la translation d'un vecteur donné correspond à l'addition de son affixe.

Une rotation d'un angle θ autour de l'origine correspond à la multiplication de l'affixe par le nombre ei θ, qui est un nombre complexe de module 1.

Une homothétie de rapport k (réel) correspond à la multiplication de l'affixe par k.

Lien externe

  • Jean-Robert Argand, Essai sur une manière de représenter des quantités imaginaires dans les constructions géométriques (1806), en ligne et commenté sur le site BibNum.
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Plan complexe ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Plan d'Argand-Cauchy de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Plan d'Argand — En mathématiques, le plan complexe (encore appelé plan de Cauchy ou plan d Argand) désigne un plan dont chaque point est la représentation graphique d un nombre complexe unique. Définition On associe en général le plan complexe à un repère… …   Wikipédia en Français

  • Plan de cauchy — Plan complexe En mathématiques, le plan complexe (encore appelé plan de Cauchy ou plan d Argand) désigne un plan dont chaque point est la représentation graphique d un nombre complexe unique. Définition On associe en général le plan complexe à un …   Wikipédia en Français

  • Plan complexe — En mathématiques, le plan complexe (encore appelé plan de Cauchy ou plan d Argand) désigne un plan dont chaque point est la représentation graphique d un nombre complexe unique. Définition On associe en général le plan complexe à un repère… …   Wikipédia en Français

  • Reperage dans le plan et dans l'espace — Repérage dans le plan et dans l espace Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Repérage dans le plan et dans l'espace — Les éléments du triplet (x,y,z) sont respectivement appelés abscisse (x), une ordonnée (y) et une cote (z). En géométrie analytique, tout point du plan ou de l espace est « repéré », c est à dire qu on lui associe un couple (dans le… …   Wikipédia en Français

  • Jean-Robert Argand — Pour les articles homonymes, voir Argand. Jean Robert Argand, né le 18 juillet 1768 à Genève et mort le 13 août 1822 à Paris, est un mathématicien (amateur) suisse. En 1806, alors qu il tient une librairie à Paris, il publie une interprétation… …   Wikipédia en Français

  • Jean-robert argand — Pour les articles homonymes, voir Argand. Jean Robert Argand, né le 18 juillet 1768 à Genève et mort le 13 août 1822 à Paris, est un mathématicien suisse. En 1806, alors qu il tient une librairie à Paris, il publie une interprétation géométrique… …   Wikipédia en Français

  • Nombre complexe — Pour les articles homonymes, voir complexe. En mathématiques, les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels …   Wikipédia en Français

  • Arithmétique complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”