Perspective axonométrique

Une commode en perspective axonométrique.

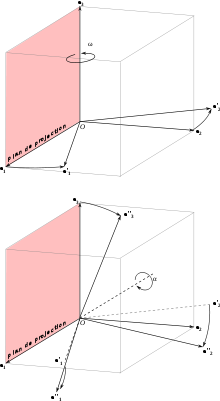
En dessin technique et en architecture, une perspective parallèle, ou perspective cylindrique ou perspective axonométrique est une forme de représentation en dimension deux d'objets en dimension trois qui a pour objectif de conserver l'impression de volume ou de relief. Appelée aussi parfois perspective rapide ou perspective artificielle, elle est différente de la perspective conique et ne représente pas ce que l’œil voit réellement : en particulier les parallèles restent représentées par des parallèles et les distances ne sont pas réduites par l'éloignement. On peut la considérer comme une perspective conique ou centrale dont le centre aurait été envoyé à l'infini, c'est-à-dire loin de l'objet observé.

Un dessin en perspective parallèle est le résultat d'un projection sur un plan parallèlement à une direction donnée.

Parmi les perspectives parallèles les plus classiques, on peut citer la perspective cavalière et l'axonométrie orthogonale (associée à une projection orthogonale). Le terme d'axonométrie, ou perspective axonométrique (de axon axe et métrie mesure) désigne selon les auteurs, ou bien une perspective parallèle quelconque, ou bien une perspective orthogonale.

Trois droites (Ox, Oy, Oz) orthogonales et graduées de la même manière définissent un repère orthonormé de l'espace. La perspective parallèle est alors entièrement déterminée par

• la donnée des images [ox'), [oy'), [oz') des trois demi-droites du repère tracée dans un même plan. En général, on représente verticalement l'axe [oz')
• la donnée des trois facteurs de réduction (k_x, k_y, k_z) à opérer sur l’échelle de chacun de ces axes.

Un point M de l'espace de coordonnées (x, y, z) sera alors représenté par le point m obtenu en se déplaçant successivement à partir du point o suivant les directions [ox'), [oy') et [oz') des distances respectives x×k_x, y×k_y et z×k_z.

Ce type de dessin est particulièrement simple à réaliser, que ce soit à la main ou par informatique (infographie, dessin assisté par ordinateur, synthèse d'image 3D). Il permet de donner une impression de relief tout en conservant les proportions dans une direction donnée. C'est pourquoi, c'est un outil utile en architecture et en dessin technique.

Inventaire

Comparaison entre différentes axonométries

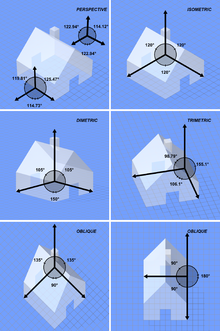
Le choix des directions des trois axes ainsi que les facteurs à opérer sur les longueurs des trois axes sont laissées au libre arbitre des dessinateurs. Parmi des pratiques très diverses, associées à un vocabulaire mal stabilisé^[1], on distingue cependant certaines perspectives privilégiées.

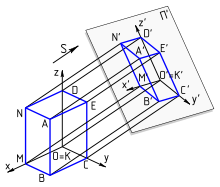
Le cas général et le théorème de Pohlke

Principe de l'axonométrie: le pavé se projeté sur le plan Π' selon la direction S, l'image obtenue est une perspective axonométrique du pavé

Un dessin en perspective parallèle est le résultat d'une projection sur un plan (P) selon une direction (d) quelconque. Un repère orthonormé (O, U, V, W) se projette en (o, u, v, w), définissant ainsi trois axes du plan (ou), (ov), (ow) gradués selon les longueurs ou, ov, ow. Un point M de l'espace de coordonnées (x, y, z) se projette alors dans le plan selon le point m du plan vérifiant l'égalité vectorielle

Pour retrouver la position de M, connaissant celle de m, il est nécessaire de connaitre une donnée supplémentaire comme par exemple l'image m₁ du projeté M₁ du point M sur le plan (OUV)^[2].

Réciproquement, Karl Pohlke (de) a démontré que 4 points non alignés (o, u, v, w) d'un plan pouvait être considéré, à ne homothétie près, comme les projetés des 4 points (O, U, V, W) de deux repères orthonormés symétriques l'un de l'autre par rapport au plan (P)^[3]. Ceci permet donc de construire une perspective parallèle en choisissant arbitrairement 4 points (o, u, v, w) ou trois axes gradués de manière inégale, censés représenter le repère de l'espace.

L'axonométrie oblique

C'est une perspective parallèle pour laquelle la direction de projection (d) n'est pas perpendiculaire au plan (P). Ce type de perspective a tendance à faire perdre les proportions entre les objets représentés et Aubert les déconseille dans le cadre du dessin d'architecte^[4]. En particulier, une sphère se projette, en projection oblique, suivant une ellipse.

Parmi les axonométries obliques, on distingue cependant deux perspectives souvent utilisées dans lesquelles la projection s'effectue sur un plan parallèle à un plan de base. Les figures situées dans des plans parallèles à ce plan de base sont alors représentées en vraies grandeurs, sans déformation.

• la perspective cavalière :cette perspective correspond à une projection sur le plan de face. L'axe vertical, et l'axe horizontal principal sont représentés sans déformation, sont perpendiculaire et sont gradués à l'identique, alors que le troisième axe, représentant la fuyante fait un angle en général de 45° ou 30° avec l'horizontale et est gradué selon une échelle plus petite (1/2 ou 0,7)
• la perspective militaire : cette perspective correspond à une projection sur un plan horizontal. Elle s'apparente à la vue que l'on pourrait avoir du terrain du haut d'une montgolfière. Les deux axes horizontaux sont représentés sans déformation, sont perpendiculaire et sont gradués à l'identique, alors que le troisième axe représentant l'axe vertical est dessiné parallèlement au bord de la feuille de papier^[5].

Ces perspectives dans lesquelles deux axes sur trois sont gradués à l'identique s'appellent des perspectives dimétriques.

L'axonométrie orthogonale

L'axonométrie orthogonale ou axonométrie droite est une perspective parallèle dans laquelle la direction de la projection (d) est perpendiculaire au plan (P). Elle permet de respecter davantage les proportions. En particulier, la sphère y est représentée par un cercle. On peut encore choisir de manière arbitraire la direction des trois axes (ou), (ov) et (ow). On choisit en général de représenter l'axe (ow) vertical et on précise alors les angles , et . Mais, les directions étant choisies, les graduations sur les trois axes sont alors imposées et se déterminent soit par le calcul soit par construction géométrique.

Le choix des angles α et β est laissé à la discrétion du dessinateur qui cherche à obtenir le meilleur rendu pour son dessin. Quand deux angles sont égaux, les échelles sur deux axes sont identiques, on parle alors de dimétrie. Lorsque les trois angles sont égaux, l'échelle sur les trois axes est identique, on parle d'isométrie ou perspective isométrique. Lorsque la perspective a pour but de rendre compte d'un plafond, privilégiant une vue en contre plongée, on parle d'axonométrie plafonnante.

Parmi les dimétries, celles dont les angles sont 97°, 131,5° et 131,5° offrent l'avantage de fournir des coefficients de réduction proportionnels à 1,1, 1/2. La perspective isométrique, dont la mise en œuvre est encore plus simple offre l'avantage de respecter les proportions mais a le fâcheux effet de confondre certains sommets du cube unité.

Usages

Tracé à la main, la perspective, même rapide demande minutie et réflexion. C'est la raison pour laquelle, pendant longtemps ne sont utilisés que des types très figées de perspective parallèles. Le développement de l'informatique et le dessin assisté par ordinateur permet une variabilité plus grande des angles de vue et rend le dessin en perspective plus rapide à exécuter.

Perspective axonométrique et vision

Dès lors que l'objet à représenter est vu sous un angle ou une profondeur importantes, la perspective conique présente un réalisme supérieur.

En effet, lorsqu'on utilise une perspective axonométrique, l'éloignement par rapport à l'observateur se traduit uniquement par une translation dans le plan et il n'y a pas de diminution de la taille des objets avec la distance.

En conséquence l'axonométrie ne pourra donner une représentation assez fidèle que :

• Si l'objet représenté est peu profond, l'effet de raccourcissement perspectif étant alors peu important.
• Si l'objet représenté est vu sous un angle raisonnablement faible.

Perspective axonométrique et arts plastiques

vers 1430 - Départ de l'empereur Ming Xuande - Détail.

voir le tableau complet ici

La perspective parallèle est utilisée de manière empirique avant que ne se mettent en place les règles de perspective conique. On peut en voir des exemples dans certaines décorations de vases grecs, dans les carnets de Villard de Honnecourt., ou dans des tableaux d'Ambrogio Lorenzetti^[6]

En Orient, les peintures chinoises et japonaises ont beaucoup utilisé l'axonométrie. Cette technique permet en effet de représenter continument des évènements consécutifs et d'en rendre compte sur des rouleaux, un peu à la manière utilisée en occident pour la tapisserie de Bayeux.

Elle permet aussi la représentation de scènes extrêmement étendues.

Matthäus Merian - 1628 - Vue de Francfort - Les lignes parallèles dans la réalité sont représentées parallèles sur le dessin, ce qui est le propre des perspectives axonométriques, et rend mal l'effet de perspective dès que les dimensions de l'objet représenté sont importantes.

Architecture

En architecture, la perspective parallèle vient compléter les vues développées par Monge qui sont la vue de face et la vue de dessus de la géométrie descriptive. Longtemps, seules les vues géométrales étaient utilisées, la perspective conique mettant en scène le bâtiment dans son environnement était plutôt réservée au domaine de l'art et de la peinture. Fidèle à ce que l'oeil voit, la perspective conique ne permettait pas d'indiquer clairement les rapport entre les diverses dimensions indispensables pour un architecte, elle est cependant utilisée par de grands noms comme Ledoux, , Lequeu,ou Viollet-le-Duc.

Jacques Ier Androuet du Cerceau, perspective cavalière des Tuileries.

Les premières représentations en perspective parallèle apparaissent au XVI^e siècle sous la plume d'Androuet du Cerceau qui construit des perspectives cavalières empiriques. Le vénitien Giovanni Battista Belluzzi exprime dans Nuova inventione di fabricar fortezze di varie forme publié en 1598, l'intérêt de l'axonométrie pour l'art des constructions militaires « parce que nous avons la nécessité de voir la chose entière, distincte et claire »^[7] et Jacques Perret de Chambéry l'utilise dans ses dessins techniques et précise que les différentes dimensions peut alors se prendre simplement au compas^[8], ce dernier utilise des perspectives militaires.

Au XIX^e siècle, c'est surtout à l'étranger que se développe une étude sérieuse de l'axonométrie avec les ouvrages de William Farish (en)^[9], en Angleterre, de Julius Weisbach^[10] et de Karl Pohlke (de)^[11] en Allemagne. L'axonométrie est défendue en France par Jules Maillard de La Gournerie^[12]. Mais c'est Auguste Choisy qui, à la fin du XIX^e siècle lui donne ses lettres de noblesse dans ses livres L'Art de construire ... ou L'Art de bâtir....

En France dans le début du XX^e siècle, l'axonométrie reste peu utilisée dans les écoles d'architecture. Faire une axonométrie rapide consiste souvent à élever des verticales sur un plan déjà tracé et à construire ainsi une perspective militaire^[13]. C'est en Allemagne que la représentation en axonométrie prend la statut d'art à part entière avec le mouvement du Bauhaus ainsi que chez des artistes du mouvement De Stijl comme Theo van Doesburg. L'axonométrie est défendue par le peintre architecte Lazar Lissitzky, dans un célèbre article K und Pangeometrie^[14]. Elle est utilisée par Giuseppe Terragni, le Corbusier et Gabriel Guevrekian (en). À partir des années 1970, elle a droit de cité comme vue complémentaire au même titre que la photographie ou la perspective conique^[15].

Dessin industriel

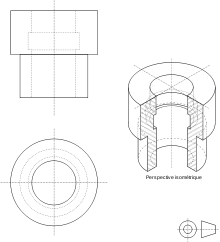Perspective isométrique d'une pièce d'outillage: les figures de gauche représentent les vues en géométrie descriptive ; la figure de droite représente une perspective isométrique avec une coupe

Les qualités géométriques des perspectives parallèles, conservation du parallélisme, conservation des proportions dans une direction fixée, en font un outil intéressant dans le dessin technique, aussi bien en mathématiques pour illustrer une configuration dans l'espace que dans le domaine industriel pour décrire les caractéristiques d'une pièce. Déjà au XI^e siècle, en Chine, on trouve dans un traité d'architecture , le Ying Tsao Fa Shih des dessins d'assemblage en perspective cavalière^[16]. Son usage a persisté même lorsque la perspective conique a offert une possibilité de représentation plus réaliste. Pour réaliser leur schéma mathématique ou leur plan de machine, c'est la perspective parallallèle que choisissent Léonard de Vinci^[17] et Lucas Pacioli, tous les deux pourtant tout-à-fait maîtres de la perspective conique. La difficulté de réaliser à la main les pièces à représenter a limité la perspective à quelques types particuliers : perspective cavalière avec une fuyante de 45° ou 60°, coefficient de réduction de 0,5 ou 0,7, ou bien une perspective isométrique. Mais l'outil informatique généralise et facilite dorénavant son usage.

Défauts des perspectives axonométriques

Comme pour toutes les projections et toutes les perspectives, la perte de l'information contenue dans la troisième dimension rend possibles certaines erreurs d'interprétation, erreurs contre lesquelles notre vue est mieux prévenue grâce à la vision binoculaire et à la possibilité que nous avons de bouger les yeux et la tête.

Tribarre de Reutersvärd

La perspective cylindrique est mieux adaptée que la conique à la représentation d'illusions perspectives, du fait qu'en plus d'être une projection elle ignore l'effet de raccourcissement perspectif. Ceci a été utilisé pour créer des objets impossibles, notamment par O. Reutersvärd et M. C. Escher.

Aspect mathématique

Formalisme

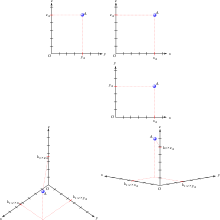
Considérons un repère orthonormé direct , les vecteurs définissant respectivement dans l'espace les axes des x, des y et des z.

Ces trois axes sont représentés par trois axes du plan du dessin, de vecteurs directeurs unitaires , et tels que :

• la représentation de est  ;
• la représentation de est  ;
• la représentation de est .

Si l'on connaît les coordonnées (x, y, z) d'un point dans l'espace, alors le placement de ce point sur le plan de projection s'obtiendra simplement en reportant ses coordonnées sur les axes projetés affectées des coefficients k₁, k₂ et k₃.

Projections orthogonales

Exemple de projection orthogonale

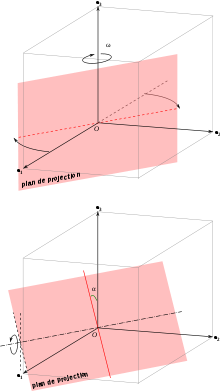
La projection orthogonale est une opération mathématique. Dans le cas qui nous intéresse, il s'agit de projeter un point de l'espace sur un plan, perpendiculairement à ce plan.

Par exemple, l'ombre créée par le Soleil, lorsque celui-ci est à la verticale de l'endroit où l'on se trouve, est une projection orthogonale de l'objet.

Les projections orthogonales sont des applications linéaires, ce qui signifie entre autres que deux vecteurs proportionnels restent proportionnels une fois projetés ; ce sont donc bien des perspectives axonométriques.

Si la projection peut se gérer simplement en infographie, la détermination des directions des axes projetés et des coefficients de proportionnalité pour le tracé manuel n'est pas très simple dans le cas général. On utilise de fait fréquemment des perspectives dimétriques pour lesquelles deux des coefficients sont égaux.

Détermination des directions des axes et des rapports

Rotations du plan de projection

Rotations du repère ayant le même effet

On peut décrire le plan de projection par des rotations transformant un plan donné, par exemple le plan (Oxz). Si l'on s'impose que la projection de reste verticale, alors on voit que le plan de projection peut s'obtenir par deux rotations, par exemple :

1. une rotation autour de l'axe (Ox) ;
2. puis une rotation autour de la projection de (Oz) sur le plan.

On peut aussi procéder dans « l'ordre inverse » :

1. une rotation autour de (Oz) ;
2. puis une rotation autour de la trace du plan (Oxy) sur le plan de projection.

C'est cette deuxième manière de faire que nous allons retenir. Remarquons que l'on obtient le même résultat en considérant que le plan de projection reste fixe, mais que c'est le repère qui tourne (avec des angles opposés). Considérons que le plan de projection est (Oxz). Si l'on opère une rotation autour de (Oz) d'un angle ω, les vecteurs de la base se transforment en :

Si l'on applique ensuite une rotation d'angle α autour de l'axe Ox initial (qui est bien la trace de (Oxy) sur le plan de projection) puis que l'on fait la projection sur le plan, on voit que, étant le repère orthonormé direct du plan de projection (transformé de par les rotations si c'est le plan qui tourne, ou bien originel si c'est le repère qui tourne) :

• le vecteur se projette selon  ;
• le vecteur se projette comme lui-même ;
• la projection du vecteur est .

Les projections axes sont donc données par les vecteurs suivants, dont la norme est le coefficient de report :

• Ox :  ;
• Oy :  ;
• Oz :  ; k₃ = | cos α | .

Les angles des axes projetés et par rapport à l'horizontale peuvent se calculer à l'aide de la trigonométrie, par exemple :

les angles étant ici non orientés.

Si x, y et z sont les coordonnées d'un point de l'espace dans le repère , et x" et y" les coordonnées de son projeté dans le repère , on peut définir la matrice P de la projection telle que

(voir l'article Produit matriciel), avec

et

Par exemple, pour ω = 30° et α = 20°, on a :

• k₁ ≈ 0,88 ;
• k₂ ≈ 0,58 ;
• k₃ ≈ 0,94 ;
• (i, e"₁) ≈ 11,17°
• (i, e"₂) ≈ 30,64°
• x" ≈ 0,87·x - 0,50·y ;
• y" ≈ -0,17·x - 0,30·y + 0,94·z.

Projections orthogonales dimétriques

Report des coordonnées pour placer un point sur une perspective dimétrique

Plan de projection tournant autour de la deuxième bissectrice du plan xy

Choisissons k₁ = k₂ ; les projections des axes x et y sont symétriques par rapport à la verticale. Cette situation est un cas particulier de la projection orthogonale avec ω = 45 ° ; on a cos ω = sin ω = √2/2, soit

• Ox :  ;  ; (i, e"₁) = arctan(sin α) ;
• Oy :  ; k₂ = k₁ ; (i, e"₂) = (i, e"₁) ;
• Oz :  ; k₃ = | cos α | .

Le plan de projection tourne autour de la deuxième bissectrice du plan (Oxy), c'est-à-dire autour du vecteur .

On a

et

Par exemple, pour α = 45 °, on a

• k₃ ≈ 0,71 ;
• k₁ = k₂ ≈ 0,87 ;
• (i, e"₁) ≈ 35,26 ° (vecteur e"₁ dirigé vers le bas) ;

et pour α = -10 °, on a

• k₃ ≈ 0,98 ;
• k₁ = k₂ ≈ 0,72 ;
• (i, e"₁) ≈ 9,85 (vecteur e"₁ dirigé vers le haut).

Perspective isométrique

La perspective isométrique est le cas particulier où les trois rapports sont égaux. Il s'agit d'une projection orthogonale.

On a :

k₁ = k₃

soit

en utilisant le fait que cos²α + sin²α = 1, on obtient

et donc également soit

• Ox :  ;  ; (i, e"₁) = arctan(1/√3) = 30 ° ;
• Oy :  ; k₂ = k₁ ; (i, e"₂) = (i, e"₁) ;
• Oz :  ; k₃ = k₁.

Il s'agit donc d'un projection orthogonale dimétrique (ω = 45 °), pour laquelle on a α ≈ 35,26 ° et k₁ = k₂ = k₃ ≈ 0,82.

et

soit

x" ≈ 0,71·(x - y )

y" ≈ -0,41·(x + y ) + 0,82·z

Projection orthogonale en synthèse d'image

On voit que si l'on connaît les coordonnées X_3D, Y_3D et Z_3D du point dans l'espace, ses coordonnées sur l'écran X_2D et Y_2D, en considérant une projection orthogonale, seront de la forme :

X_2D = X_2D_0 + facteur*( A1*X_3D + A2*Y_3D )

Y_2D = Y_2D_0 + facteur*( B2*(A2*X_3D - A1*Y_3D) + B1*Z_3D )

où X_2D_0 et Y_2D_0 sont des constantes permettant de « centrer » l'image, et facteur est une constante d'échelle. Les constantes A1, A2, B1 et B2 caractérisent la direction des axes et les proportion des reports sur ces axes ; ils peuvent être définis par :

A1 = cos(omega)

A2 = sin(omega)

B1 = cos(alpha)

B2 = sin(alpha)

omega et alpha étant des constantes (par rapport à l'étude précédente, le signe pour sin ω a changé, ce qui correspond à un changement du signe des angles, donc à la référence pour le sens de rotation). On peut aussi les définir sans relation avec les angles, de manière « empirique » (par exemple ajustés par essais-erreur pour obtenir un résultat « agréable »), comme étant compris entre -1 et 1 et vérifiant :

A1^2 + A2^2 = 1

B1^2 + B2^2 = 1

on peut ainsi ne définir que deux paramètres, A1 et B1, et calculer :

A2 = sqrt(1 - A1^2) ou A2 = - sqrt(1 - A1^2)

B2 = sqrt(1 - B1^2) ou B2 = - sqrt(1 - B1^2)

Notes et références

Bibliographie

• Jean Aubert, Axonométrie : Théorie, art et pratique des perspective parallèles: axonométrie orthogonale, axonométrie oblique, perspective cavalière et militaire, complétées d'une brève histoire orientée de l'axonométrie, éditions de la Villette (ISBN 2903539383) 

Voir aussi

• Portail de la géométrie