Paradoxe des anniversaires

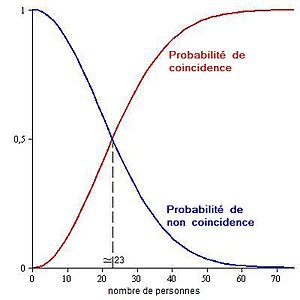
Le paradoxe des anniversaires, dû à Richard von Mises, est à l'origine une estimation probabiliste du nombre de personnes que l'on doit réunir pour avoir une chance sur deux que deux personnes de ce groupe aient leur anniversaire le même jour de l'année. Il se trouve que ce nombre est 23, ce qui choque un peu l'intuition. À partir d'un groupe de 57 personnes, la probabilité est supérieure à 99 %.

Cependant, il ne s'agit pas d'un paradoxe dans le sens de contradiction logique ; c'est un paradoxe, dans le sens où c'est une vérité mathématique qui contredit l'intuition : la plupart des gens estiment que cette probabilité est très inférieure à 50 %.

(Par souci de simplicité, tout l'article est rédigé en supposant que toutes les années sont non-bissextiles. Prendre en compte le 29 février changerait peu les résultats, mais rendrait les calculs très délicats pour les applications où les personnes ne sont pas nées la même année)

Comprendre le problème

La clé consiste à se demander quelles sont les chances qu'aucune paire de personnes soit née le même jour. Pour chaque personne ajoutée dans la pièce, le nombre de dates non déjà prises diminue. La première personne a donc 365 choix, la deuxième 364, la troisième 363, la quatrième 362, et ainsi de suite.

Le problème consiste à se demander si une quelconque paire d'individus dans la pièce a la même date d'anniversaire.

Dans un groupe de vingt-trois personnes, il y a 23 × 22 ÷ 2 = 253 paires possibles, ce qui représente plus de la moitié du nombre de jours contenu dans une année. À partir de 28, le nombre de paires excède le nombre de jours, ce qui ne signifie évidemment pas qu'il est impossible de trouver un groupe de 28 personnes dont l'anniversaire est différent. En effet, le nombre de paires donne une intuition du problème mais n'explique pas la probabilité associée car cela reviendrait à additionner les probabilités d'évènements qui ne sont pas disjoints.

Généralisation

Ce paradoxe des anniversaires se généralise à la situation plus abstraite que l'on peut énoncer sous la forme :

Soit $E$ un ensemble fini. La probabilité $p (n)$ que, parmi $n$ éléments de $E$ , chaque élément étant tiré uniformément dans tout l'ensemble $E$ , deux éléments au moins soient identiques vaut :

$p(n)=1 - \frac{|E|!}{(|E|-n)!} \cdot \frac{1}{|E|^n}$

où la notation $| E |$ désigne le nombre d'éléments de l'ensemble $E$ .

Une valeur approchée est donnée par

$p(n)\approx 1 - e^{-\frac{n(n-1)}{2\cdot |E|}}$

et une valeur de $n$ en fonction de $p$ par

$n(p)\approx \sqrt {2\cdot |E| \ln\left(\frac{1}{1-p}\right)}$

Démonstration

Nous donnons une preuve pour le cas d'origine, avec des jours d'anniversaires, mais cela se transpose simplement au cas de la généralisation énoncé.

Le plus simple pour obtenir le résultat annoncé est de calculer la probabilité que chaque personne ait un jour anniversaire différent de celui des autres. On va procéder par dénombrement, c'est-à-dire, que nous allons compter le nombre de cas où $n$ personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Il y a $n$ personnes, pour chacune il y a 365 jours possibles, donc au total si on ne se fixe aucune contrainte, il a $365 n$ possibilités. Si maintenant on veut des jours différents, nous obtenons un arrangement de $n$ parmi 365, soit : $A^n_{365}=(365-0)(365-1)...(365-n+1)=\frac{365!}{(365-n)!}$ .

On a donc

$\overline{p}(n)= \frac{365!}{(365-n)!} \cdot \frac{1}{365^n}$

On peut également le voir comme une multiplication de probabilités d'événements indépendants:

$\overline{p}(n)= \underbrace{ \frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \cdots \cdot \frac{365-n+1}{365} }_\text{n facteurs}$

Or, l'événement « un jour anniversaire différent par personne » est le complémentaire de « au moins deux identiques ». Par conséquent la probabilité recherchée est $p(n)=1-\overline{p}(n)$ .

En faisant l'application numérique, on trouve 50,73 % pour vingt-trois personnes.

Probabilité de coïncidence de 2 anniversaires en fonction du nombre de personnes.

n	p(n)
5	2,71 %
10	11,69 %
15	25,29 %
20	41,14 %
25	56,87 %
30	70,63 %
40	89,12 %
50	97,04 %
60	99,41 %
80	99,99 %
100	99,99997 %
200	99,9999999999999999999999999998 %
300	$\left(1 - \left(7 .10^{-73}\right)\right)\cdot100\%$
350	$\left(1 - \left(3 . 10^{-131}\right)\right)\cdot100\%$
>365	100 % (par le Principe des tiroirs)

Paires trompeuses

Lorsqu'on effectue le calcul par intuition, en comptant le nombre de paires, on omet le fait que les évènements ne sont pas disjoints.

Prenons l'exemple pour trois personnes (Alain, Bernard et Charles). En les prenant deux à deux, la probabilité d'avoir la même date d'anniversaire est 1/365. Et donc pour les trois paires, on aurait 3/365. Cependant, en faisant ce calcul, on oublie que l'anniversaire des trois personnes peut avoir lieu le même jour. Définissons trois évènements : A: Alain et Bernard ont leur date d'anniversaire en commun B: Bernard et Charles ont leur date d'anniversaire en commun C: Charles et Alain ont leur date d'anniversaire en commun. Et donc, $P (A) = P (B) = P (C) = 1 / 365$ . Ce que nous cherchons c'est la probabilité d'avoir l'évènement A ou B ou C, soit $P(A \cup B \cup C)$ . En utilisant le formalisme repris dans les axiomes des probabilités.

$P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(B \cap C) - P(C \cap A) - P(A \cap B) + P(A \cap B \cap C).$

Comme les éléments sont indépendants deux à deux (le fait que Charles ait son anniversaire le même jour que Bernard n'a pas d'influence sur le fait qu'il ait aussi son anniversaire en même temps qu'Alain) donc

$P(B \cap C) = P(C \cap A) = P(A \cap B) = 1/365 \cdot 1/365$

Par contre, on peut réécrire $P(A \cap B \cap C) = P(A|(B \cap C)) \cdot P(B \cap C) = P(A|(B \cap C)) \cdot P(B) \cdot P(C)$ . Or ici, $A$ et $(B \cap C)$ ne sont pas indépendants, si Bernard et Charles ont leur anniversaire en même temps et Charles et Alain aussi, alors forcément Alain et Bernard aussi, donc $P(A|(B \cap C)) = 1$ .

En résumé, on aura $P(A \cup B \cup C) = 3/365 - 2 \cdot 1/365\cdot1/365$ . Ce qui correspond bien au résultat précédent.

Etendre ce raisonnement à un plus grand nombre de personnes devient rapidement très compliqué. Cependant, on comprend mieux pourquoi il ne suffit pas d'avoir 28 personnes pour être certain d'avoir un anniversaire commun.

Approximation

p(n)

La probabilité $\overline{p}(n)=1-p(n)$ peut se réécrire sous la forme :

$\overline{p}(n)=\left(1-\frac{0}{365}\right)\left(1-\frac{1}{365}\right)...\left(1-\frac{i}{365}\right)...\left(1-\frac{n-1}{365}\right)$

Or, on a le développement limité $e x = 1 + x + o (x)$ pour $x$ voisin de 0. Cela conduit à l'approximation :

$\overline{p}(n)\approx \prod_{i=0}^{n-1}e^{-\frac{i}{365}}$

$\overline{p}(n)\approx e^{-\frac{ \sum_{i=0}^{n-1} i}{365}}$

Or, la somme des entiers de 0 à $n - 1$ vaut $(n - 1) n / 2$ , ce qui donne finalement :

$\overline{p}(n)\approx e^{-\frac{ n(n-1)}{2\cdot 365}}$

En revenant à $p (n)$ :

$p(n)\approx 1- e^{-\frac{ n(n-1)}{2\cdot 365}}$

n(p)

L'approximation de $p (n)$ permet d'obtenir simplement une approximation du nombre de personnes nécessaire pour avoir une probabilité donnée $p$ d'avoir au moins deux personnes avec le même jour d'anniversaire. On obtient ainsi :

$n(p)\approx \sqrt{2\cdot 365\ln\left(\frac{1}{1-p}\right)}$

Quelques valeurs numériques

Le tableau ci-dessous indique, pour une probabilité $p$ , l'approximation $n (p)$ , puis, sur la même ligne, l'approximation de la probabilité pour l'entier inférieur ou égal à $n (p)$ (noté $\lfloor n\rfloor$ ) et celle de probabilité pour l'entier supérieur ou égal à $n (p)$ (noté $\lceil n\rceil$ ). Normalement, la probabilité $p$ fixée au départ doit être comprise entre ces deux valeurs. Les entrées ne vérifiant pas cette condition sont signalées en couleur.

$p$	$n$	$\lfloor n\rfloor$	$p(\lfloor n\rfloor)$	$\lceil n\rceil$	$p(\lceil n\rceil)$
0,01	2,70864	2	0,00274	3	0,00820
0,05	6,11916	6	0,04046	7	0,05624
0,1	8,77002	8	0,07434	9	0,09462
0,2	12,76302	12	0,16702	13	0,19441
0,3	16,13607	16	0,28360	17	0,31501
0,5	22,49439	22	0,47570	23	0,50730
0,7	29,64625	29	0,68097	30	0,70632
0,8	34,27666	34	0,79532	35	0,81438
0,9	40,99862	40	0,89123	41	0,90315
0,95	46,76414	46	0,94825	47	0,95477
0,99	57,98081	57	0,99012	58	0,99166

Applications

Dans Le Trésor des Paradoxes (Éd Belin, 2007), les auteurs notent que l’informaticien américain Robert Mac Eliece a établi l'intérêt du paradoxe des anniversaires en informatique, pour s’assurer de la fiabilité des mémoires d’ordinateur, grâce à des codes détecteurs d’erreurs, fondés notamment sur les travaux de Richard Hamming aux Laboratoires Bell. La stratégie des codes détecteurs d’erreurs s’avère, du point de vue statistique, similaire au paradoxe des anniversaires. Le paradoxe des anniversaires est utilisé en cryptographie pour élaborer des attaques sur les fonctions de hachage. Une des contraintes imposées sur ces fonctions, pour une utilisation cryptographique, est de produire peu de collisions, autrement dit, de rarement prendre la même valeur sur des entrées différentes.

Le paradoxe des anniversaires donne une borne sur le nombre moyen d'éléments nécessaires pour avoir une collision avec une probabilité $p=\frac{1}{2}$ , à savoir essentiellement la racine carrée du nombre de valeurs possibles pour la fonction de hachage, sous l'hypothèse que cette fonction est uniformement distribuée sur ses valeurs d'arrivée.

Plus concrètement, si une fonction de hachage a une sortie de N bits alors l'ensemble d'arrivée possède $2 N$ éléments et il faut environ $2^\frac N2$ hachés d'éléments distincts pour produire une collision avec 50 % de chance ; les sorties de la fonction pouvant être comparées à des personnes avec des anniversaires se répartissant sur $2 N$ valeurs.

Anecdote

Dans Le Livre qui rend fou, Raymond Smullyan raconte que lui-même a fait établir la formule à ses 19 élèves. Il conclut après application numérique qu'il y a nettement moins d'une chance sur deux (un peu moins de 38%) pour que deux élèves aient leur anniversaire le même jour. Un élève lui répond qu'il parie que c'est tout de même le cas. Le professeur fait l'appel en demandant aux élèves de donner leur date de naissance, et éclate de rire avant la fin, suivi de toute la classe, en se souvenant que deux de ses élèves sont jumeaux.

Voir aussi

Lien externe

Programme écrit en Maple donnant la probabilité que n personnes soient nés des jours différents

v · Preuve de sécurité • Sécurité inconditionnelle • IND-CPA • IND-CCA • Kerckhoffs • Malléabilité • Sécurité calculatoire • Hypothèses calculatoires • Confusion et diffusion
Cryptanalyse de base	Biais statistique • Corrélation • Dictionnaire • Force brute • Fréquence • Indice de coïncidence • Interpolation • Mot probable
Cryptanalyse par canal auxiliaire	Acoustique • Consommation • Émanations EM • Faute • Sondage • Temporel
Cryptanalyse ciblée	Clé apparentée • Clé faible • EFF • Enigma • Glissement • Intégrale • Linéaire / Différentielle / Différentielle impossible / Différentielle-linéaire / Boomerang • Modes opératoires • Modulo n • Quadratique • Rectangle • Rencontre au milieu • Vigenère • χ²
Systèmes asymétriques	Clé apparentée • Clé faible • Homme au milieu • Sécurité sémantique
Fonctions de hachage	Effet avalanche • Linéaire / Différentielle • Paradoxe des anniversaires • Pseudo-collision
Autres	Anonymat • Confidentialité • Intégrité • Sécurité par l'obscurité

Portail des probabilités et des statistiques

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Paradoxe des anniversaires de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Paradoxe de l'anniversaire — Paradoxe des anniversaires Le paradoxe des anniversaires, dû à Richard von Mises, est à l origine une estimation probabiliste du nombre de personnes que l on doit réunir pour avoir une chance sur deux que deux personnes de ce groupe aient leur… … Wikipédia en Français
Paradoxe — Pour l’article homophone, voir Paradox. Les « cubes impossibles » de M. Escher sont des représentations graphiques paradoxales. Un paradoxe, d après l étymologie (d … Wikipédia en Français
Paradoxe probabiliste — Les paradoxes probabilistes sont les problèmes de la théorie des probabilités largement contre intuitifs ou tout simplement présentant différents résultats selon l interprétation que l on fait de l énoncé parmi plusieurs possibilités légitimes ou … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Sécurité matérielle des cartes à puce — La sécurité matérielle des cartes à puce et des autres microcontrôleurs est l un des éléments clefs de la sécurité des informations sensibles qu ils manipulent. La littérature scientifique a produit un grand nombre de publications visant à… … Wikipédia en Français
EFF DES Cracker — Deep Crack, circuit dédié à l attaque par force brute de DES. En cryptographie, l EFF DES cracker (surnommé Deep Crack) est une machine spécialisée dans l attaque du DES, construite en 1998 par l EFF. Le but était de prouver que la clé du DES n… … Wikipédia en Français
EFF DES cracker — Deep Crack, circuit dédié à l attaque par force brute de DES. En cryptographie, l EFF DES cracker (surnommé Deep Crack) est une machine spécialisée dans l attaque du DES, construite en 1998 par l EFF. Le but était de prouver que la clé du DES n… … Wikipédia en Français
Eff des cracker — Deep Crack, circuit dédié à l attaque par force brute de DES. En cryptographie, l EFF DES cracker (surnommé Deep Crack) est une machine spécialisée dans l attaque du DES, construite en 1998 par l EFF. Le but était de prouver que la clé du DES n… … Wikipédia en Français
Intégrité des données — Intégrité (cryptographie) Sommaire 1 Intégrité des données 2 Intégrité d un système 3 Articles connexes 4 Liens externes … Wikipédia en Français
Sécurité logicielle des cartes à puce — La sécurité logicielle des cartes à puce fournit aux applications de ce domaine les moyens de se protéger des comportements dévoyés de logiciels malveillants. Les cartes à puce embarquent des systèmes d exploitation qui implémentent des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'