Paradoxe des deux chèques

Le paradoxe des deux enveloppes repose sur un raisonnement subtilement fallacieux, mais clairement et incontestablement identifiable. En cela, ce n'est nullement un paradoxe, mais un bon exercice de raisonnement probabiliste.

Sommaire 1 Énoncé 2 Explications 3 Voir aussi 3.1 Articles connexes 3.2 Liens externes 3.3 Bibliographie

Énoncé

Deux enveloppes contiennent chacune un chèque. On sait que l'un des chèques porte un montant double de l'autre. Le candidat choisit une des enveloppes.

Avant qu'il n'ouvre l'enveloppe, on lui demande s'il souhaite changer d'enveloppe.

Soit N la valeur du chèque dans l'enveloppe choisie en premier. Il y a deux cas possibles :

• une chance sur deux que l'autre enveloppe contienne un chèque deux fois plus important (donc de valeur 2N);
• une chance sur deux que l'autre enveloppe contienne un chèque deux fois plus petit (donc de valeur N / 2).

L'espérance de gain si on change d'enveloppe paraît donc être 0,5 * 2N + 0,5 * N / 2, soit 1,25N, qui est supérieur à N. Il faudrait donc à tout coup changer d'enveloppe.

Or un tel choix parait absurde, puisque les enveloppes ne se distinguent entre elles que par leur nom. On s'attendrait à ce que les enveloppes gardent une espérance de gain égale après ces manipulations indépendantes de leur contenu.

D'ailleurs, si on répétait la manœuvre (rechanger l'enveloppe pour reprendre la même) , le calcul s'applique encore et on serait censé avoir 1,25 * 1,25N, alors qu'on a retrouvé l'enveloppe initiale !

Explications

Tout le paradoxe est basé sur une présentation trompeuse : d'abord elle occulte le fait que la valeur de N est différente selon l'enveloppe qu'on a déjà en main ; ensuite, le calcul ne tient pas compte de la perte engendrée par l'abandon de l'enveloppe initiale.

Or, il est normal que l'espérance de gain rapportée à la valeur initiale, donc en pourcentage, soit différente selon l'enveloppe qu'on a en main ! Dans un cas, on gagne 100%, dans le second, on perd 50%, pour faire correctement la moyenne il ne faut pas faire, comme proposé : 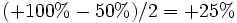mais pondérer par les valeurs initiales :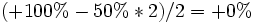

On retrouve le fait qu'après une hausse de 100%, il suffit d'une baisse de 50% pour retrouver le montant initial.

Une autre présentation du raisonnement correct est la suivante

• une chance sur deux que l'autre enveloppe contienne un chèque deux fois plus important (donc de valeur 2N) : le changement fait perdre N et gagner 2N, gain total : N ;
• une chance sur deux que l'autre enveloppe contienne un chèque deux fois plus petit (donc de valeur N / 2), : le changement fait gagner N/2 et perdre N, gain total : -N/2 (négatif, c'est une perte), mais où N vaut le double du cas précédent.

L'espérance de gain par changement d'enveloppe est donc 0,5 * N + 0.5 * (2 * ( − N / 2)) = 0. On ne gagne rien .

On peut augmenter le nombre d'enveloppes, de contenus respectifs divers, le problème reste le même. En revanche le problème serait différent si une enveloppe était ouverte après le choix initial. Il faudrait dans ce cas tenir compte de la valeur pour évaluer la probabilité d'avoir initialement tiré le plus gros chèque.

Voir aussi

Articles connexes

• Problème de Monty Hall

Liens externes

• (fr)David Madore, Un peu de probabilités
• (en)David J. Chalmers, The Two-Envelope Paradox: A Complete Analysis?

Bibliographie

• (en) [pdf] Albers, Trying to resolve the two-envelope problem, Chapter 2 of his thesis Distributional Inference: The Limits of Reason, December 2002