Cryptanalyse Intégrale

Cryptanalyse Intégrale

Cryptanalyse intégrale

La cryptanalyse intégrale est une technique formalisée par David Wagner et Lars Knudsen pour attaquer des chiffrements insensibles à la cryptanalyse différentielle. Elle nécessite de disposer d'un grand nombre de paires de textes clairs et chiffrés. Le but est de prédire la valeur des intégrales après un certain nombre de tours dans un chiffrement de bloc.

Sommaire

Explication mathématique

Dualité avec la cryptanalyse différentielle

La cryptanalyse intégrale est la duale de la cryptanalyse différentielle dans le sens où l'on ne s'intéresse pas aux propagations de différences dans la structure de chiffrement mais à la somme de plusieurs valeurs. L'opération d'intégration utilisée dans ce type d'attaque est à mettre en rapport avec son équivalent analytique. Toutefois une différence majeure apparaît : on considère un nombre fini de vecteurs dans le cas de la cryptanalyse intégrale.

Formellement, si l'on considère un ensemble fini 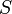S~ de vecteurs, chaque composante d'un vecteur provient d'un groupe abélien additif si bien qu'il est possible d'additionner les vecteurs composante par composante. On peut ainsi formuler une définition de l'intégrale qui est équivalente à l'addition vectoriel classique en géométrie :

\int S = \sum_{v \in S} v = (\sum_{v \in S} v^1, \sum_{v \in S} v^2, ..., \sum_{v \in S} v^n)

Séparation des cas

Plusieurs cas sont considérés :

  1. la ne composante est identique pour tous les vecteurs
  2. la ne composante est différente pour tous les vecteurs
  3. l'intégrale des vecteurs aboutit à une valeur connue à l'avance

Par l'application de divers théorèmes, des informations peuvent être obtenues à partir du résultat de l'intégrale. Si le nombre de vecteurs considérés est égale à l'ordre du groupe et que la n-ième composante est constante pour tous les vecteurs alors la n-ième composante de l'intégrale sera l'élément neutre du groupe (par exemple : 1+1+1+1 = 0 mod 4, 2+2+2+2 = 0 mod 4, etc.)

Applications

Knudsen et Wagner donnent un exemple sur Rijndael en considérant 256 textes clairs de 16 octets chacun (128 bits, soit la taille du bloc de Rijndael). Les textes partagent 15 octets qui sont identiques pour tous les textes, le 16e diffère pour chacun d'entre eux (ce qui fait 256 textes distincts au final).

On chiffre chacun des messages avec trois tours de Rijndael. On obtient 256 sorties de 16 octets (valeurs partiellement chiffrées) qui correspondent aux vecteurs précédemment évoqués. En intégrant ces 256 vecteurs, on obtient un vecteur dont les composantes sont toutes identiques. Cela permet de mener une attaque sur quatre tours en procédant à une intégration lors du déchiffrement (on modifie un seul octet de la clé et on regarde si l'octet dans l'intégration est en concordance avec l'octet de l'intégration lors du chiffrement).

La cryptanalyse intégrale a également fait ses preuves sur d'autres chiffrements comme MISTY1, SAFER ou Square.

Liens externes

Mesures de sécurité cryptographique
Cryptographie Preuve de sécurité • Sécurité inconditionnelle • IND-CPA • IND-CCA • Kerckhoffs • Malléabilité • Sécurité calculatoire • Hypothèses calculatoires • Confusion et diffusion
Cryptanalyse de base Biais statistique • Corrélation • Dictionnaire • Force brute • Fréquence • Indice de coïncidence • Interpolation • Mot probable
Cryptanalyse par canal auxiliaire Acoustique • Consommation • Émanations EM • Faute • Sondage • Temporel
Cryptanalyse ciblée Clé apparentée • Clé faible • EFF • Enigma • Glissement • Intégrale • Linéaire / Différentielle / Différentielle impossible / Différentielle-linéaire / Boomerang • Modes opératoires • Modulo n • Quadratique • Rectangle • Rencontre au milieu • Vigenère • χ²
Systèmes asymétriques Clé apparentée • Clé faible • Homme au milieu • Sécurité sémantique
Fonctions de hachage Effet avalanche • Linéaire / Différentielle • Paradoxe des anniversaires • Pseudo-collision
Autres Anonymat • Confidentialité • Intégrité • Sécurité par l'obscurité
  • Portail de la cryptologie Portail de la cryptologie
Ce document provient de « Cryptanalyse int%C3%A9grale ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cryptanalyse Intégrale de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Cryptanalyse integrale — Cryptanalyse intégrale La cryptanalyse intégrale est une technique formalisée par David Wagner et Lars Knudsen pour attaquer des chiffrements insensibles à la cryptanalyse différentielle. Elle nécessite de disposer d un grand nombre de paires de… …   Wikipédia en Français

  • Cryptanalyse intégrale — La cryptanalyse intégrale est une technique formalisée par David Wagner et Lars Knudsen pour attaquer des chiffrements insensibles à la cryptanalyse différentielle. Elle nécessite de disposer d un grand nombre de paires de textes clairs et… …   Wikipédia en Français

  • Cryptanalyse Différentielle — La cryptanalyse différentielle est une méthode générique de cryptanalyse qui peut être appliquée aux algorithmes de chiffrement itératif par blocs, mais également aux algorithmes de chiffrement par flots et aux fonction de hachage. Dans son sens… …   Wikipédia en Français

  • Cryptanalyse differentielle — Cryptanalyse différentielle La cryptanalyse différentielle est une méthode générique de cryptanalyse qui peut être appliquée aux algorithmes de chiffrement itératif par blocs, mais également aux algorithmes de chiffrement par flots et aux… …   Wikipédia en Français

  • Cryptanalyse Linéaire — La cryptanalyse linéaire est une technique inventée par Mitsuru Matsui, chercheur chez Mitsubishi. Elle date de 1993 et fut développée à l origine pour casser l algorithme de chiffrement symétrique DES. Ce type de cryptanalyse se base sur un… …   Wikipédia en Français

  • Cryptanalyse lineaire — Cryptanalyse linéaire La cryptanalyse linéaire est une technique inventée par Mitsuru Matsui, chercheur chez Mitsubishi. Elle date de 1993 et fut développée à l origine pour casser l algorithme de chiffrement symétrique DES. Ce type de… …   Wikipédia en Français

  • Cryptanalyse Différentielle Impossible — En cryptanalyse, la cryptanalyse différentielle impossible ou cryptanalyse par différentielles impossibles est une technique basée sur la cryptanalyse différentielle (1990), elle a été proposée en 1999 par Eli Biham, Adi Shamir et Alex Biryukov… …   Wikipédia en Français

  • Cryptanalyse differentielle impossible — Cryptanalyse différentielle impossible En cryptanalyse, la cryptanalyse différentielle impossible ou cryptanalyse par différentielles impossibles est une technique basée sur la cryptanalyse différentielle (1990), elle a été proposée en 1999 par… …   Wikipédia en Français

  • Cryptanalyse par différentielles impossibles — Cryptanalyse différentielle impossible En cryptanalyse, la cryptanalyse différentielle impossible ou cryptanalyse par différentielles impossibles est une technique basée sur la cryptanalyse différentielle (1990), elle a été proposée en 1999 par… …   Wikipédia en Français

  • Cryptanalyse d’Enigma — Cryptanalyse d Enigma La cryptanalyse d Enigma, c est à dire le décryptage des messages transmis et codés par Enigma, fut fondamentale au succès des Alliés pendant la Seconde Guerre mondiale. Le mathématicien polonais Marian Rejewski a élaboré la …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”