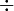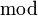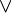PPCM (mathématiques élémentaires)

En mathématiques et plus précisément en arithmétique, le plus petit commun multiple, en abrégé PPCM (noté lcm en anglais pour least common multiple), de deux entiers naturels a et b, est le plus petit entier qui soit à la fois multiple de ces deux nombres. On le note a ∨ b^[1], ppcm(a, b), ou parfois simplement (a, b).

Le PPCM de a et b peut également se définir comme un multiple commun de a et de b qui divise tous les multiples communs de a et de b.

La définition s'étend aux entiers relatifs. Sous la seconde forme, il faut alors ajouter qu'il doit être positif. La seconde forme de la définition se généralise en fait à un anneau commutatif quelconque, mais on perd en général l'existence et l'unicité, on parle alors d'un PPCM de deux éléments. L'existence est assurée dans les anneaux factoriels.

Le PPCM peut se définir plus généralement pour un nombre quelconque d'éléments : par exemple dans les entiers naturels, le PPCM de n entiers est le plus petit entier multiple simultanément de ces n entiers.

Sommaire 1 Définition 2 Calcul 2.1 A l'aide de la décomposition avec les nombres premiers 2.2 A l'aide du PGCD 3 Notes et références 4 Articles connexes

Définition

Soient .

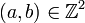• Si a=0 ou b=0
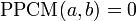
• Si a et b sont non nuls on note

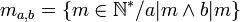
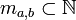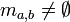On vérifie alors que et (car )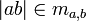

Par axiome, min(m_a,b) existe.

On définit .

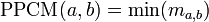Calcul

A l'aide de la décomposition avec les nombres premiers

La décomposition en facteurs premiers du PPCM de n entiers strictement positifs contient tous les nombres premiers qui apparaissent dans au moins une des décompositions en facteurs premiers de ces n entiers, chacun affecté du plus grand exposant qui apparait dans celles-ci. On obtient donc une méthode de calcul du PPCM en décomposant chaque nombre en produit de nombres premiers.

Exemple: prenons les nombres 60 et 168 et décomposons-les en produits de facteurs premiers.On a :

60=2×2×3×5=2²×3×5

168=2×2×2×3×7=2³×3×7

Pour le nombre premier 2, le plus grand exposant est 3. Pour les nombres premiers 3, 5 et 7, le plus grand exposant est 1. On a alors PPCM(60, 168)=2³×3×5×7=840

A l'aide du PGCD

Dans le cas où aucun des deux entiers a et b n'est nul, le plus petit commun multiple peut être calculé en utilisant le plus grand commun diviseur (ou PGCD) de a et b,

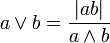qui s'écrit aussi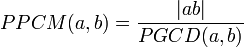

Ainsi, l'algorithme d'Euclide pour le calcul du PGCD. nous donne aussi un algorithme rapide de calcul du PPCM

Exemple: avec l'algorithme d'Euclide, calculons PGCD(60,168) :
168 = 60 × 2 + 48
60 = 48 x 1 + 12
48 = 12 × 4 + 0 .

PGCD(60,168) = 12. Donc 12 × PPCM(60;168) = 60×168, soit :

PPCM(60;168) = (60 × 168) / 12 = 840.

Notes et références

Articles connexes

• Livre VII des Éléments d'Euclide

Opérations binaires
Numériques En ensemble ordonné Structurelles Autres Élémentaires + Addition − Soustraction Multiplication Division Puissance Arithmétiques div Quotient euclidien Reste euclidien pgcd PGCD ppcm PPCM Combinatoires () Coefficient binomial A Arrangement Ensembles de parties Union Complémentation Intersection Δ Différence symétrique Ordre total min Minimum max Maximum Treillis Borne inférieure Borne supérieure Ensembles Produit cartésien Somme disjointe Puissance ensembliste Groupes Somme directe Produit libre Produit en couronne Modules Produit tensoriel Hom Homomorphisme Tor Torsion Ext Extension Arbres Enracinement Variétés connexes Somme connexe Espaces pointés Bouquet Smash produit Joint Fonctionnelles Composition de fonctions Produit de convolution Vectorielles Produit scalaire Produit vectoriel Algébriques [,] Crochet de Lie {,} Crochet de Poisson Produit extérieur Homologiques Cup produit Produit d'intersection Séquentielles + Concaténation
Logique booléenne : ET (conjonction) • OU (disjonction) • OU exclusif • IMP (implication) • EQV (équivalence)

• Portail des mathématiques