- PGCD (mathématiques élémentaires)
-
Plus grand commun diviseur (mathématiques élémentaires)

Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques Le PGCD (ou plus grand diviseur commun) de deux nombres entiers naturels non nuls est, comme son nom l’indique, le plus grand nombre entier qui divise nos deux nombres.
Considérons par exemple 30 et 48. 6 divise 30 car 6×5=30 et 6 divise 48 car 6×8=48.
Il n’y a pas de nombre entier supérieur à 6 qui divise à la fois 30 et 48 car sinon il serait divisible par 5.De la même manière on peut parler de PGCD de plusieurs nombres entiers naturels.
Sommaire
Méthode par décomposition en facteurs premiers
Pour trouver facilement le PGCD de nombres pas trop grands, il est efficace de les décomposer en produits de facteurs premiers.
Reprenons 30 et 48 :- 30=2×3×5
- 48=2×2×2×2×3
On remarque que le produit 2×3=6 est commun aux deux et est le plus grand produit commun, il est donc le PGCD.
Dans le cas de plus de deux nombres entiers cette méthode est applicable :
- 56=2×2×2×7=2³×7
- 84=2×2×3×7=2²×3×7
- 140=2×2×5×7=2²×5×7
Leur PGCD est donc 2²×7 soit 28.
Algorithme d'Euclide
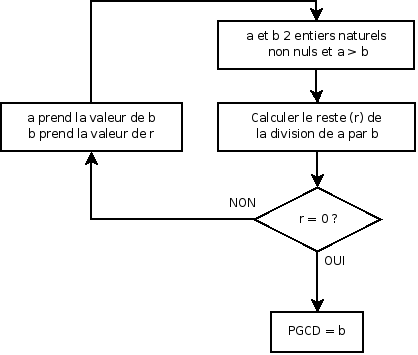
Cet algorithme est un peu plus difficile à comprendre, il s’appuie sur le fait que si un nombre entier divise deux autres nombres entiers, alors il divise leur différence (et leur somme). Il divisera donc les différences successives du plus petit ôté du plus grand.
Reprenons l’exemple de 30 et de 48 :
- 48−30=18
- 30−18=12
- 18−12=6
- 12−2×6=0
Le dernier reste non nul est le PGCD.
Essayons avec 56 et 140 :
- 140−56=84
- 84−56=28
- 56−28=28
- 28−28=0
Donc le PGCD est 28
On aurait pu présenter ce dernier de la manière suivante, avec des divisions :
- 140−2×56=28
- 56−2×28=0
Ces algorithmes s'appellent algorithme par soustractions successives et par divisions successives
Propriété
Le produit du plus grand commun diviseur et du plus petit commun multiple de deux nombres est égal au produit des deux nombres.
- PGCD(a,b) × PPCM(a,b) = a × b
comme on sait calculer le PGCD, ceci nous fournit une méthode simple pour calculer le PPCM.
Voir aussi
- Plus grand commun diviseur (article plus avancé)
- Algorithme d'Euclide
Catégorie : Mathématiques élémentaires
Wikimedia Foundation. 2010.
