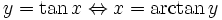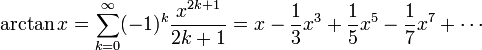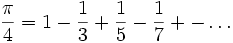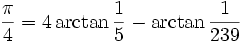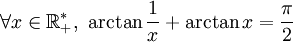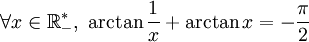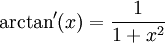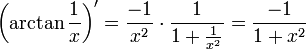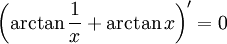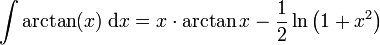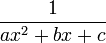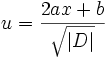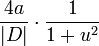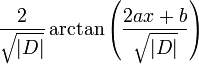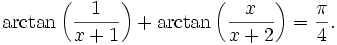Arctan

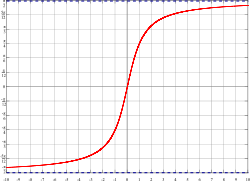
Fonction arctangente

Représentation graphique

La fonction arctangente est la fonction réciproque de la restriction de la fonction tangente à l'intervalle $]-½ π; ½π[$ . Notée naguère $arctg$ , elle se note désormais 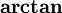$\textbf{arctan}$ . La notation $tan - 1$ , souvent utilisée sur les calculatrices de poche, est à proscrire, car elle prête à confusion avec le rapport $1 / tan$ .

Concrètement, si $x$ appartient à $]-½π ; ½π[$ et $y$ appartient à $\R$ :

$y = \tan x \Leftrightarrow x = \arctan y$

La courbe représentative de la fonction arctangente est obtenue à partir de la courbe représentative de la restriction de la fonction tangente à l'intervalle $]-½π ; ½π[$ par une réflexion d'axe la droite d'équation $y = x$ .

Sommaire

1 Développement en série de Taylor
2 Équation fonctionnelle
3 Fonction réciproque
4 Dérivée
5 Logarithme complexe
6 Intégration
- 6.1 Primitive
- 6.2 Utilisation de la fonction arctangente
7 Formule remarquable

Développement en série de Taylor

Le développement en série de Taylor de la fonction arctangente est :

$\arctan x=\sum_{k=0}^{\infty} (-1)^k\frac{x^{2k+1}}{2k+1}= x - \frac13 x^3 + \frac15 x^5 - \frac17 x^7+ \cdots$

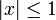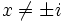Cette série entière converge quand $|x|\le 1$ et $x\neq\pm i$ . La fonction arctangente est cependant définie sur tout $\R$ .

Le développement en série peut être utilisé pour effectuer un calcul approché du nombre π : la formule la plus simple est le cas $x = 1$ , appelée formule de Leibniz

$\frac\pi4=1-\frac13+\frac15-\frac17+-\ldots$

La formule de Machin, plus sophistiquée,

$\frac\pi4=4\arctan\frac15-\arctan\frac1{239}$

fut utilisée par John Machin en 1706 pour calculer les 100 premières décimales de $π$ et par William Shanks en 1873 pour calculer les 707 premières décimales, sur lesquelles seules 527 étaient justes.

Équation fonctionnelle

De $arctan(1 ⁄ x)$ on peut déduire $arctan(x)$ et inversement :

$\forall x\in{\R_+^*},\ \arctan \frac{1}{x} + \arctan x= \frac{\pi}{2}$

$\forall x\in{\R_-^*},\ \arctan \frac{1}{x} + \arctan x= -\frac{\pi}{2}$

Ces équations fonctionnelles peuvent se prouver par exemple en montrant que la dérivée est nulle. On a :

$\arctan'(x) = \frac{1}{1+x^2}$

$\left(\arctan\frac{1}{x}\right )' = \frac{-1}{x^2} \cdot \frac{1}{1+{\frac{1}{x^2}}} = \frac{-1}{1+x^2}$

donc

$\left(\arctan \frac{1}{x} + \arctan x\right)' = 0$

On en déduit que $arctan(1 ⁄ x) + arctan(x)$ est constante par morceau sur chaque intervalle de son ensemble de définition, et on trouve facilement la valeur de cette constante en calculant la valeur prise en $x = 1$ et $x = - 1$ .

Fonction réciproque

Par définition, la réciproque $\left] -\frac{\pi}{2};\frac{\pi}{2}\right[,\ y = \arctan x \Leftrightarrow x = \tan y$

Dérivée

$\arctan'(x) = \frac{1}{1+x^2}$

que l'on démontre très facilement en dérivant les 2 membres de la relation : $tan(a r c t a n (x)) = x$

Démonstration détaillée

On utilise la formule de la dérivation d'une composée de fonction :

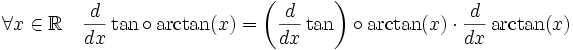
$\forall x \in \mathbb R \quad \frac d{dx} \tan\circ \arctan (x) = \left(\frac d{dx} \tan\right)\circ \arctan (x)\cdot \frac d{dx} \arctan (x)$

En utilisant la formule de la dérivée d'une tangente, on obtient :

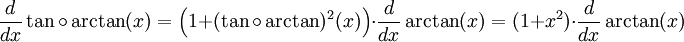
$\frac d{dx} \tan\circ \arctan (x) = \Big( 1 + (\tan \circ \arctan)^2 (x)\Big)\cdot \frac d{dx} \arctan (x)= (1+x^2)\cdot \frac d{dx}\arctan (x)$

Comme les fonctions tangente et arctangente sont réciproques, leur composition est égale à la fonction identité de dérivée constante 1. On en déduit l'expression recherchée :

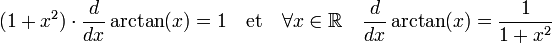
$(1+x^2)\cdot \frac d{dx}\arctan (x) = 1\quad \text{et}\quad \forall x \in \mathbb R \quad \frac d{dx}\arctan(x) = \frac 1{1+x^2}$

Logarithme complexe

On peut exprimer la fonction arctangente par un logarithme complexe :

$\arctan(x) = \frac{1}{2\mathrm i} \ln\left(\frac{1+\mathrm ix}{1-\mathrm ix}\right)$

Démonstration détaillée

On réécrit la dérivée de la fonction arctangente :

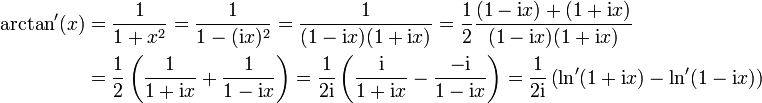
$\begin{align}\arctan'(x) & = \frac{1}{1+x^2} = \frac{1}{1-(\mathrm ix)^2} = \frac{1}{(1-\mathrm ix)(1+\mathrm ix)} = \frac{1}{2} \frac{(1-\mathrm ix)+(1+\mathrm ix)}{(1-\mathrm ix)(1+\mathrm ix)} \\ \ & = \frac{1}{2} \left(\frac{1}{1+\mathrm ix} + \frac{1}{1-\mathrm ix}\right) = \frac{1}{2\mathrm i} \left(\frac{\mathrm i}{1+\mathrm ix} - \frac{-\mathrm i}{1-\mathrm ix}\right) = \frac{1}{2\mathrm i} \left(\ln'(1+\mathrm ix) - \ln'(1-\mathrm ix)\right) \end{align}$

On intègre de chaque côté :

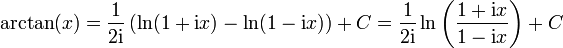
$\arctan(x) = \frac{1}{2\mathrm i} \left(\ln(1+\mathrm ix) - \ln(1-\mathrm ix)\right) + C = \frac{1}{2\mathrm i} \ln\left(\frac{1+\mathrm ix}{1-\mathrm ix}\right) + C$

Enfin, on calcule la constante d’intégration $C$ en $x = 0$ :

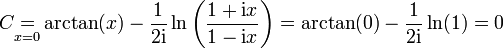
$C \underset{x=0}{=} \arctan(x) - \frac{1}{2\mathrm i} \ln\left(\frac{1+\mathrm ix}{1-\mathrm ix}\right) = \arctan(0) - \frac{1}{2\mathrm i} \ln(1) = 0$

On trouve donc finalement :

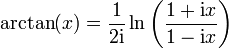
$\arctan(x) = \frac{1}{2\mathrm i} \ln\left(\frac{1+\mathrm ix}{1-\mathrm ix}\right)$

Intégration

Primitive

La primitive de la fonction arctangente est

$\int \arctan(x)\;\mathrm dx = x \cdot \arctan x - \frac{1}{2} \ln\left(1 + x^2\right)$

Utilisation de la fonction arctangente

La fonction arctangente joue un rôle important dans l'intégration des expressions de la forme

$\frac1{ax^2+bx+c}$

Si le discriminant $D = b 2 - 4 a c$ est positif ou nul, l'intégration est possible en revenant à une fraction partielle. Si le discriminant est négatif, on peut faire la substitution par

$u=\frac{2ax+b}{\sqrt{|D|}}$

qui donne pour l'expression à intégrer

$\frac{4a}{|D|}\cdot\frac1{1+u^2}$

L'intégrale est alors

$\frac{2}{\sqrt{|D|}} \arctan\left(\frac{2ax+b}{\sqrt{|D|}}\right)$

Formule remarquable

Nous avons la formule suivante :

$\arctan\left(\frac{1}{x+1}\right) + \arctan\left(\frac{x}{x+2}\right) = \frac{\pi}{4}.$

Portail des mathématiques

Ce document provient de « Fonction arctangente ».

Catégories : Trigonométrie | Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Arctan de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

arctan — arctan, Funktionszeichen für die Arkusfunktion Arkustangens … Universal-Lexikon
Arctan — Arkustangens und Arkuskotangens sind mathematische Funktionen. Sie sind die Umkehrfunktionen des Tangens bzw. des Kotangens und damit Arkusfunktionen. Da der Tangens periodisch ist, wird zur Umkehrung der Definitionsbereich von Tangens auf ( − π… … Deutsch Wikipedia
arctan — noun the inverse function of the tangent; the angle that has a tangent equal to a given number • Syn: ↑arc tangent, ↑arctangent, ↑inverse tangent • Hypernyms: ↑trigonometric function, ↑circular function * * * arctan /ärk tanˈ/ abbrev … Useful english dictionary
arctan — Invers Tangens … Acronyms
arctan — Invers Tangens … Acronyms von A bis Z
arctan — abbreviation the inverse of a tangent … English new terms dictionary
Inverse trigonometric functions — Trigonometry History Usage Functions Generalized Inverse functions Further reading … Wikipedia
Formule de Machin — La formule de Machin fut découverte en 1706 par John Machin et relie le nombre π à la fonction arctangente : Cette formule permet de calculer une approximation du nombre π grâce au développement en série entière de la fonction arctangente.… … Wikipédia en Français
Arc tangente — Représentation graphique En mathématiques, l’arc tangente d un nombre réel est la mesure d un angle orienté dont la tangente vaut ce nombre. La fonction qui à tout nombre réel associe la valeur de son arc tangente en radians est la réciproque de… … Wikipédia en Français
Arctangente — Fonction arctangente Représentation graphique La fonction arctangente est la fonction réciproque de la restriction de la fonction tangente à l intervalle ] ½π; ½π[. Notée naguère arctg, elle se note désormais … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'