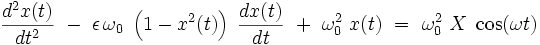Oscillateur de van der pol
- Oscillateur de van der pol
-
Oscillateur de Van der Pol
L'oscillateur de Van der Pol est un système dynamique différentiable à temps continu et à un degré de liberté, du nom de Balthasar van der Pol. Il est décrit par une coordonnée x(t) vérifiant une équation différentielle faisant intervenir deux paramètres :
- une pulsation propre ω0 ;
- un coefficient de non-linéarité ε.
Lorsque ε = 0, cet oscillateur se réduit à un oscillateur harmonique pur.
Oscillateur libre
L'équation différentielle de l'oscillateur libre s'écrit :
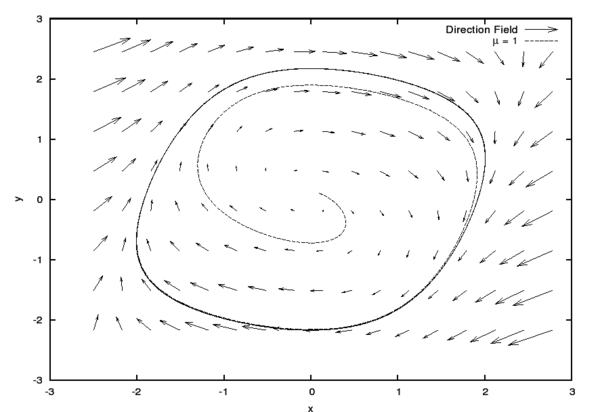
Lorsque 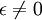 , ce système dissipatif possède une dynamique régulière caractérisée par un attracteur en forme de cycle limite, représenté sur la figure ci-dessous (où on a posé ω0 = 1) :
, ce système dissipatif possède une dynamique régulière caractérisée par un attracteur en forme de cycle limite, représenté sur la figure ci-dessous (où on a posé ω0 = 1) :
Oscillateur forcé
Lorsque cet oscillateur est excité par un terme harmonique à la pulsation ω, son équation différentielle devient :
à développer ...
Articles connexes
Liens externes
Bibliographie
- Balth. van der Pol & J van der Mark ; The Heartbeat considered as a Relaxation oscillation, and an Electrical Model of the Heart, Philosophical Magazine Supplement 6 (1928), 763-775.
- Shawnee L. Mc Murran & James J. Tattersall ; Cartwright and Littlewood on van der Pol's equation, Harmonic analysis and nonlinear differential equations (Riverside, CA, 1995), Contemporary Mathematics 208, American Mathematical Society (Providence, RI, 1997), 265-276.
Notes
 Portail des mathématiques
Portail des mathématiques Portail de la physique
Portail de la physique
Catégories : Système dynamique remarquable | Méthode mathématique de la physique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Oscillateur de van der pol de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Oscillateur de Van der Pol — L oscillateur de Van der Pol est un système dynamique différentiable à temps continu et à un degré de liberté, du nom de Balthasar van der Pol. Il est décrit par une coordonnée x(t) vérifiant une équation différentielle faisant intervenir deux… … Wikipédia en Français
Balthasar Van Der Pol — (Utrecht, 27 janvier 1889 6 octobre 1959 Wassenaar), physicien expérimentateur. Sommaire 1 Carrière 2 Œuvres 3 Articles connexes 4 Bibliographie … Wikipédia en Français
Balthasar van der pol — (Utrecht, 27 janvier 1889 6 octobre 1959 Wassenaar), physicien expérimentateur. Sommaire 1 Carrière 2 Œuvres 3 Articles connexes 4 Bibliographie … Wikipédia en Français
Balthasar van der Pol — (Utrecht, 27 janvier 1889 6 octobre 1959 Wassenaar), physicien expérimentateur, est connu pour ses travaux sur les oscillations non linéaires, qui ont connu depuis les années 1980 un regain d intérêt à la faveur de la théorie du chaos. Sommaire 1 … Wikipédia en Français
Oscillateur — Un oscillateur harmonique vertical non amorti. En physique, un oscillateur est un système évoluant de part et d autre d un équilibre stable. Les variations des grandeurs décrivant le système peuvent être périodiques dans le temps (ou pseudo… … Wikipédia en Français
Systeme dynamique — Système dynamique Pour consulter un article plus général, voir : Systèmes dynamiques. En mathématiques, en physique théorique et en ingénierie, un système dynamique est un système classique[1] qui évolue au cours du temps de façon à la… … Wikipédia en Français
Système dynamique — Ne doit pas être confondu avec Dynamique des systèmes (en) Pour consulter un article plus général, voir : théorie des systèmes dynamiques. En mathématiques, en physique théorique et en ingénierie, un système dynamique est un… … Wikipédia en Français
Cycle Limite — En mathématiques, dans l étude des systèmes dynamiques, on appelle cycle limite, ou cycle limite sur un plan ou une variété bidimensionnelle une trajectoire fermée dans l espace des phases, telle qu au moins une autre trajectoire spirale à l… … Wikipédia en Français
Cycle limite — En mathématiques, dans l étude des systèmes dynamiques, on appelle cycle limite, ou cycle limite sur un plan ou une variété bidimensionnelle une trajectoire fermée dans l espace des phases, telle qu au moins une autre trajectoire spirale à l… … Wikipédia en Français
Chaotique — Théorie du chaos Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys … Wikipédia en Français
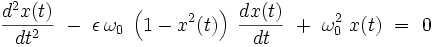
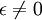 , ce système dissipatif possède une dynamique régulière caractérisée par un attracteur en forme de cycle limite, représenté sur la figure ci-dessous (où on a posé ω0 = 1) :
, ce système dissipatif possède une dynamique régulière caractérisée par un attracteur en forme de cycle limite, représenté sur la figure ci-dessous (où on a posé ω0 = 1) :