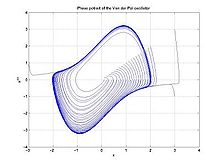
- Cycle limite
-
En mathématiques, dans l'étude des systèmes dynamiques, on appelle cycle limite, ou cycle-limite sur un plan ou une variété bidimensionnelle une trajectoire fermée dans l'espace des phases, telle qu'au moins une autre trajectoire spirale à l'intérieur lorsque le temps tend vers
.On observe de tels comportements dans l'étude de certains systèmes non-linéaires. Si toutes les trajectoires voisines approchent le cycle limite lorsque t
, on parle de cycle limite stable ou attractif. Si en revanche cela se produit lorsque t 
, on parle de cycle limite instable ou non-attractif.Les cycles limites stables impliquent des oscillations maintenues. Toute perturbation qui éloignerait la trajectoire du cycle limite s'atténuerait avec le temps, pour revenir à ce cycle limite quand
.Sommaire
Cas de l'oscillateur de Van der Pol
Cycle limite de l'oscillateur de Van der Pol
On peut observer un cycle limite stable pour l'oscillateur de Van der Pol. Toutes les trajectoires tendent à former une figure fermée : le système a tendance à maintenir des oscillations.
Cas général
Le nombre de cycles limites d'une équation différentielle polynomiale fait l'objet de la seconde partie du 16ème problème de Hilbert. Le théorème de Poincaré-Bendixson et celui de Bendixson-Dulac prédisent l'existence, respectivement l'absence, de cycles limites pour les équations différentielles non-linéaires sur deux dimensions.
Voir aussi
- plan de phase
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Limit-cycle » (voir la liste des auteurs)
- Steven H. Strogatz, « Nonlinear Dynamics and Chaos », Addison Wesley publishing company, 1994 ;
- M. Vidyasagar, « Nonlinear Systems Analysis », second edition, Prentice Hall, Englewood Cliffs, New Jersey 07632 ;
- Philip Hartman, « Ordinary Differential Equation », Society for Industrial and Applied Mathematics, 2002 ;
- Witold Hurewicz, « Lectures on Ordinary Differential Equations », Dover, 2002 ;
- Solomon Lefschetz, « Differential Equations: Geometric Theory », Dover, 2005 ;
- Lawrence Perko, « Differential Equations and Dynamical Systems », Springer-Verlag, 2006 ;
Wikimedia Foundation. 2010.
