Opération à droite

En mathématiques, une loi de composition externe dans un ensemble E à opérateurs (ou scalaires) dans S ( on dit aussi plus brièvement une loi externe de S sur E ) est une relation ternaire externe de S sur E qui est aussi une application.

Sommaire 1 Définition 2 Principales propriétés 2.1 Propriétés simples 2.2 Propriétés relatives à une loi interne 3 Voir aussi

Définition

Suivant que S vient en premier ou en second lieu dans le produit cartésien qui sert d'ensemble de départ à la loi externe considérée, on distingue les lois externes à gauche et à droite. Ainsi :

• une loi externe à gauche de S sur E est une application de S × E dans E ;
• une loi externe à droite de S sur E est une application de E × S dans E .

Principales propriétés

Propriétés simples

Soit un ensemble E muni d'une loi externe « . » à scalaires dans un ensemble S. Nous considérerons le cas d'une loi à gauche (resp. à droite).

• la loi « . » est exo-unifère à gauche (resp. exo-unifère à droite), ou plus simplement unifère ssi il existe un élément de S qui, composé par cette loi avec tout élément de E , redonne l'élément de E

ou :

- pour une relation à gauche :

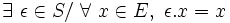
- et à droite :

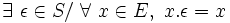
• la loi « . » est absorbante à droite (resp. absorbante à gauche ), ou plus simplement absorbante ssi il existe un élément de E qui, composé par cette loi avec tout élément de S , se redonne lui-même

ou :

- pour une relation à gauche :

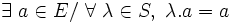
- et à droite :

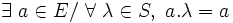
• la loi « . » est exo-absorbante à gauche (resp. exo-absorbante à droite), ou plus simplement exo-absorbante ssi il existe un élément de E et un élément de S tels que l'élément de E soit l'unique résultat de la composition de l'élément de S avec tout élément de E

ou :

- pour une relation à gauche :

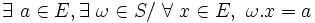
- et à droite :

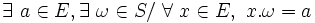
• la loi « . » est régulière à gauche (resp. à droite ) ssi pour chaque élément de S , ses composés par cette loi avec les éléments de E sont tous distincts entre eux

ou :

- pour une relation à gauche :

- et à droite :

• la loi « . » est exo-régulière à droite (resp. à gauche ) ssi pour chaque élément de E, ses composés par cette loi avec les éléments de S sont tous distincts entre eux

ou :

- pour une relation à gauche :

- et à droite :

• la loi « . » est régulière ssi elle est régulière d'un côté et exo-régulière de l'autre.

Propriétés relatives à une loi interne

• la loi « . » est exo-associative par rapport à une loi interne « 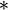 » de S si tout composé par la loi « . » d'un scalaire avec le composé par la loi « . » d'un autre scalaire et d'un élément de E est égal au composé de cet élément de E avec le composé des deux scalaires par la loi «  »

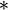ou :

- pour une relation à gauche :

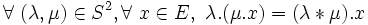
- et à droite :

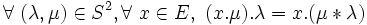
• la loi « . » est distributive ( à gauche ( resp. à droite )) par rapport à une loi interne «  » de E si tout composé par la loi « . » d'un scalaire avec le composé par la loi «  » de deux éléments de E est égal au composé par la loi « 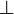 » des deux composés par la loi « . » de ces éléments de E avec le scalaire précédent

ou :

- pour une relation à gauche :

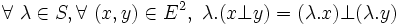
- et à droite :

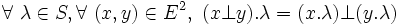
• la loi « . » est exo-distributive ( à droite ( resp. à gauche )) par rapport à une loi interne « 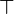 » de S relativement à une autre loi interne «  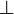» de E si tout composé par la loi « . » d'un élément de E avec le composé par la loi «  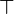» de deux scalaires est égal au composé par la loi «  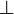» des deux composés par la loi « . » de l'élément de E avec chaque scalaire

ou :

- pour une relation à gauche :

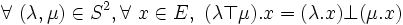
- et à droite :

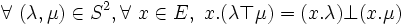
Voir aussi

• Loi de composition

• Portail des mathématiques