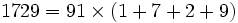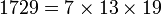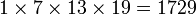- Nombre de Hardy-Ramanujan
-
1729 (nombre)
1 729 (mille sept cent vingt-neuf) est l'entier naturel qui suit 1728 et précède 1730.
1 729 Cardinal mille sept cent vingt-neuf Ordinal mille sept cent vingt-neuvième
1729ePréfixe grec Préfixe latin Adverbe Mille sept cent vingt-neuvièmement Adverbe d'origine
latineMultiplicatif d'origine
latinePropriétés Facteurs premiers 7×13x19 Diviseurs 7, 13, 19, 91, 133, 247 Autres numérations Numération romaine MDCCXXIX Système binaire 11011000001 Système octal 3301 Système duodécimal 1001 Système hexadécimal 6C1 Sommaire
Propriétés
Nombre de Hardy-Ramanujan
1 729 est également connu sous le nom de « nombre de Hardy-Ramanujan » ; il s'agit du plus petit entier naturel s'écrivant de deux manières différentes comme somme de deux cubes :
- 1729 = 123 + 13 = 103 + 93
Il s'agit donc du nombre taxicab d'ordre 2.
Bien qu'elle ait été découverte en 1657 par Bernard Frénicle de Bessy, la propriété de 1 729 ainsi que son nom sont liées à une anecdote relatée par le mathématicien britannique Godfrey Harold Hardy après une visite à son collègue indien hospitalisé Srinivasa Ramanujan, en 1917 :
- « Je me souviens d'une fois où j'arrivai à son chevet à Putney. J'avais été conduit par le taxi numéro 1 729 ; la morosité qui semblait émaner de ce nombre avait attiré mon attention. J'espérais qu'il ne constituait pas un mauvais présage. "Non , me répondit-il, c'est un nombre fort intéressant ; c'est le plus petit que l'on puisse exprimer comme somme de deux cubes de deux manières différentes." »
Il existe des entiers naturels plus petits que 1 729 pouvant s'écrire de deux manières différentes comme somme de deux cubes d'entiers relatifs, comme 91 ou 189 :
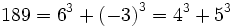 et
et 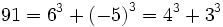 .
.Autres propriétés
1 729 est également :
- Le troisième nombre de Carmichaël, c'est-à-dire un nombre pseudo-premier vérifiant la propriété du petit théorème de Fermat.
- Un nombre Harshad en bases 8, 10 et 16, c'est-à-dire divisible par la somme de ses chiffres :
- Un nombre de Zeisel, c'est-à-dire que ses facteurs premiers sont au moins trois et suivent une progression arithmético-géométrique (ici, une progression arithmétique de raison 6) :
- Un nombre polygonal, plus précisément dodécagonal, 24-gonal, et 84-gonal.
- Le produit d'un nombre premier: 19 , par son inversé : 91
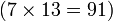
- La position du début de l'emplacement dans les décimales de e de la séquence 0719425863 qui est la première occurrence d'une séquence de longueur 10 contenant chaque chiffre une et une seule fois[1].
- L'un des quatre nombres (les autres sont 81, 1458 et 1) dont la somme des chiffres multipliée par le nombre inversé redonne le nombre de départ[1] :
- 1 + 7 + 2 + 9 = 19;
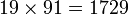
- 1 + 7 + 2 + 9 = 19;
- Le treizième nombre de la forme[1] :
- n3 + 1
- Le neuvième nombre de la forme[1] :
- n3 + (n + 1)3
- Le quatrième nombre « factoriel sextuple »[1], c'est à dire un produit de termes successifs de la forme
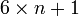 :
:
- La somme des diviseurs d'un carré parfait[1] :
- 332
Références
- G. H. Hardy, A Mathematician's Apology, Cambridge University Press (1940). 153 pages. ISBN 0-521-42706-1.
Notes
Voir aussi
- Personnages cités :
- Propriétés remarquables :
Catégories : Nombre entier | 1729
Wikimedia Foundation. 2010.