Nombre de Carmichaël

En théorie des nombres, un nombre de Carmichael est un entier composé positif n qui vérifie la propriété 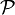suivante :

pour tout entier a, n est un diviseur de aⁿ − a

Sommaire 1 Tour d'horizon 1.1 Propriétés 1.2 Démonstration du théorème de Korselt 2 Nombres de Carmichael d'ordre supérieur 2.1 Propriétés 3 Références 4 Lien externe

Tour d'horizon

Le petit théorème de Fermat énonce que les nombres premiers ont la propriété 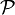. Sa réciproque est fausse, les nombres de Carmichael sont les nombres positifs qui satisfont à 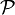sans être premiers, ce sont des menteurs de Fermat ; l'existence de tels nombres pseudopremiers absolus est ce qui empêche d'utiliser le test de primalité de Fermat pour prouver qu'un nombre est composé.

Plus les nombres deviennent grands et plus les nombres de Carmichael deviennent rares, la majorité d'entre eux rendent le test de primalité de Fermat largement inutile comparé aux autres tests de primalité comme le test de primalité de Solovay-Strassen. Par exemple, le 646^e nombre de Carmichael vaut 993 905 641 et il existe 105 212 nombres de Carmichael entre 1 et 10¹⁵.

Une caractérisation des nombres de Carmichael est donnée par le théorème de Korselt en 1899.

Théorème (Korselt 1899) : Un entier positif composé n est un nombre de Carmichael si et seulement si aucun carré de nombre premier ne divise n (on dit que n est quadratfrei (sans carré)) et pour chaque diviseur premier p de n, le nombre p − 1 divise n − 1.

Il découle de ce théorème que tous les nombres de Carmichael sont des produits d'au moins trois nombres premiers impairs différents.

Korselt fut le premier à observer ces propriétés, mais il n'a pas pu trouver d'exemples de nombre de Carmichael. En 1910, Robert Daniel Carmichael trouva le plus petit de ces nombres, 561, et ceux-ci furent nommés en son honneur.

Ce nombre de Carmichael 561 peut être vérifié avec le théorème de Korselt. Effectivement, 561 = 3 · 11 · 17 n'est pas divisible par un carré de nombre premier, et 3 - 1 = 2, 11 - 1 = 10 et 17 - 1 = 16 sont tous trois des diviseurs de 560.

Les premiers nombres de Carmichael sont :

561 = 3 · 11 · 17

1 105 = 5 · 13 · 17

1 729 = 7 · 13 · 19

2 465 = 5 · 17 · 29

2 821 = 7 · 13 · 31

6 601 = 7 · 23 · 41

8 911 = 7 · 19 · 67

La suite des 33 premiers nombres de Carmichael en ordre croissant est donnée par la suite n°A002997 de l'Encyclopédie électronique des suites entières (OEIS), et la suite des 19 279 premiers nombres de Carmichael (classés par ordre croissant et décomposés en leurs facteurs premiers) est donnée ici.

J. Chernick démontra un théorème en 1939 qui peut être utilisé pour construire un sous-ensemble de nombres de Carmichael. Le nombre (6k + 1)(12k + 1)(18k + 1) est un nombre de Carmichael si ses trois facteurs sont tous premiers. On ne sait pas si cette formule, ou d'autres similaires, engendre une infinité de nombres de Carmichael lorsque k décrit l'ensemble des entiers.

Paul Erdős soutint de manière heuristique qu'il devrait y exister une infinité de nombres de Carmichael. Cette conjecture a été démontrée en 1994 par William Alford, Andrew Granville et Carl Pomerance, et même, plus précisément, pour un n suffisamment grand, il existe au moins n^2/7 nombres de Carmichael compris entre 1 et n.

Richard G. E. Pinch démontra quant à lui que pour tout n, il n'y a pas plus de 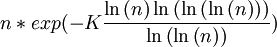nombres de Carmichael compris entre 1 et n avec K une constante donnée.

Le tableau suivant donne les valeurs approximatives de cette constante:

n	K
4	2,19547
6	1,97946
8	1,90495
10	1,86870
12	1,86377
14	1,86293
16	1,86406
18	1,86522
20	1,86598

Tel qu'en décembre 2007, il a été montré qu'il existe 8220777 nombres de Carmichael jusqu'à 10²⁰

Propriétés

Les nombres de Carmichael ont au moins trois facteurs premiers.

Les premiers nombres de Carmichael avec respectivement au moins k = 3, 4, 5,... facteurs premiers sont (suite A006931 de l'OEIS) :

k
3	561 = 3 · 11 · 17
4	41041 = 7 · 11 · 13 · 41
5	825265 = 5 · 7 · 17 · 19 · 73
6	321197185 = 5 · 19 · 23 · 29 · 37 · 137
7	5394826801 = 7 · 13 · 17 · 23 · 31 · 67 · 73
8	232250619601 = 7 · 11 · 13 · 17 · 31 · 37 · 73 · 163
9	9746347772161 = 7 · 11 · 13 · 17 · 19 · 31 · 37 · 41 · 641

Les premiers nombres de Carmichael avec quatre facteurs premiers sont (suite A074379 de l'OEIS) :

i
1	41041 = 7 · 11 · 13 · 41
2	62745 = 3 · 5 · 47 · 89
3	63973 = 7 · 13 · 19 · 37
4	75361 = 11 · 13 · 17 · 31
5	101101 = 7 · 11 · 13 · 101
6	126217 = 7 · 13 · 19 · 73
7	172081 = 7 · 13 · 31 · 61
8	188461 = 7 · 13 · 19 · 109
9	278545 = 5 · 17 · 29 · 113
10	340561 = 13 · 17 · 23 · 67

Une coïncidence amusante est la suivante : le troisième nombre de Carmichael, 1729, n'est autre que le nombre de Hardy-Ramanujan, c'est-à-dire le plus petit entier positif qui peut être écrit de deux façons différentes comme la somme de deux cubes (1729 = 10³ + 9³ = 12³ + 1³). Dans la même veine, le deuxième nombre de Carmichael, 1105, peut être écrit comme somme de deux carrés de plus de façons que n'importe quel entier qui lui est inférieur. Pour clôturer la séquence, le premier nombre de Carmichael 561 peut (comme n'importe quel entier naturel) s'écrire comme somme de puissances unaires d'entiers positifs de plus de façons que n'importe quel entier positif plus petit.

Démonstration du théorème de Korselt

Soit p un nombre premier qui divise un nombre de Carmichael n. On a (p+1)ⁿ=1+np+C_n²p²+...≡1 (mod p²). D'autre part (p+1)ⁿ≡pⁿ+1 ≡ p+ 1(mod n) (La deuxième congruence découle du fait que n est un nombre de Carmichael). Si p² divisait n, on aurait 1≡(p+1)ⁿ≡p+1 (mod p²) ce qui est impossible. Cela montre que le carré de p ne divise pas n.

n étant un nombre de Carmichael, et p un facteur premier de n, soit a une racine primitive de p (a fortiori a premier avec p). 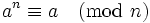donc 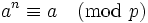car p divise n, soit encore 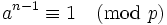puisque a est premier avec p. On en déduit que n-1 est multiple de l'ordre de a modulo p, c'est-à-dire de p-1. Donc pour tout nombre de Carmichael n, chacun de ses facteurs premiers p vérifie que p-1 divise n-1.

Réciproquement, supposons que n soit un produit de nombres premiers tous distincts, p₁, p₂, ... p_k et que les nombres p₁-1, p₂-1, ... divisent tous n-1. Alors pour tout entier a et tout p_i on a n≡1 (mod p_i-1) et donc a≡a^p_i ≡a^2p_i-1 ≡a^3p_i-2≡...≡aⁿ (mod p_i). Le nombre aⁿ est congru à a modulo chacun des p_i, donc aussi modulo leur produit n. C'est vrai pour tout entier a, donc n est un nombre de Carmichael.

Ceci achève la démonstration du théorème de Korselt.

Conséquences du théorème de Korselt :

Soit n un nombre de Carmichael. Il est divisible par plusieurs nombres premiers disctints, donc l'un d'eux au moins est différent de deux. Appelons p ce diviseur premier impair de n. Puisque p-1 est pair, son multiple n-1 l'est aussi. Cela montre que tout nombre de Carmichael est impair.

Si p est un facteur premier d'un nombre de Carmichael n, alors modulo p-1 on a p≡1≡n et donc 1≡(n/p)p≡(n/p)1=n/p. Autrement dit, si p est un facteur premier d'un nombre de Carmichael, alors le produit des autres facteurs premiers est congru à 1 modulo p-1.

Un nombre de Carmichael ne peut être le produit de deux nombres premiers p et q, car alors chacun des deux nombres p-1 et q-1 diviserait l'autre et ils seraient égaux.

Tout nombre de Carmichael est donc le produit d'au moins trois nombres premiers impairs distincts.

Nombres de Carmichael d'ordre supérieur

Les nombres de Carmichael peuvent être généralisés en utilisant les concepts de l'algèbre générale.

La définition ci-dessus énonce qu'un entier composé n est un nombre de Carmichael précisément lorsque la fonction nième puissance p_n de l'anneau Z_n des entiers modulo n dans lui-même est la fonction identité. L'identité est le seul Z_n-endomorphisme d'algèbre sur Z_n donc nous pouvons rétablir la définition en demandant que p_n soit un endomorphisme d'algèbre de Z_n. Comme ci-dessus, p_n satisfait à la même propriétés quand n est premier.

La fonction nième puissance p_n est aussi définie sur n'importe quel Z_n-algèbre A. Un théorème énonce que n est premier si et seulement si toutes les fonctions telles que p_n sont des endomorphismes d'algèbres.

Entre ces deux conditions se trouve la définition du nombre de Carmichael d'ordre m pour n'importe quel entier positif m comme n'importe quel nombre composé n tel que p_n est un endomorphisme sur chaque Z_n-algèbre qui peut être générée comme un Z_n-module par m éléments. Les nombres de Carmichael d'ordre 1 sont simplement les nombres de Carmichael ordinaires.

Propriétés

Le critère de Korselt peut être généralisé aux nombres de Carmichael d'ordre supérieur, voir l'article de Howe ci-dessous.

Un argument heuristique, donné dans le même article, semble suggérer qu'il existe une infinité de nombres de Carmichael d'ordre m, quel que soit m. Néanmoins, on ne connaît aucun nombre de Carmichael d'ordre 3 ou plus.

Références

• Chernick, J. (1935). On Fermat's simple theorem. Bull. Amer. Math. Soc. 45, 269–274.
• Howe, Everett W. (2000). Higher-order Carmichael numbers. Mathematics of Computation 69, 1711–1719. (online version)

Lien externe

• Wikisource:Carmichael_numbers
• Mathpages: The Dullness of 1729
• Liste des nombres de Carmichael de moins de treize chiffres [1]
• Richard G.E. Pinch. The Carmichael numbers up to 10 to the 20. (liste des publications)

• Portail des mathématiques