- Nombre cyclique
-
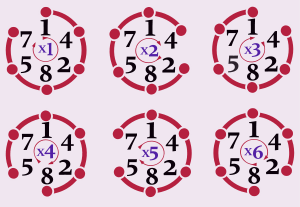
Un nombre cyclique, ou nombre phénix, est un entier dont les permutations circulaires des chiffres correspondent aux multiples du nombre. Le plus connu est 142857:
- 142857 × 1 = 142857
- 142857 × 2 = 285714
- 142857 × 3 = 428571
- 142857 × 4 = 571428
- 142857 × 5 = 714285
- 142857 × 6 = 857142
Sommaire
Cas spéciaux
Si les zéros ne sont pas permis au début des nombres, alors 142857 est le seul nombre cyclique décimal. Par contre, s'ils sont permis, la séquence des nombres cycliques commence comme suit :
- 142857 (6 chiffres)
- 0588235294117647 (16 chiffres)
- 052631578947368421 (18 chiffres)
- 0434782608695652173913 (22 chiffres)
- 0344827586206896551724137931 (28 chiffres)
- 0212765957446808510638297872340425531914893617 (46 chiffres)
- 0169491525423728813559322033898305084745762711864406779661 (58 chiffres)
- 016393442622950819672131147540983606557377049180327868852459 (60 chiffres)
Pour être cyclique, seuls les multiples successifs du nombre doivent être considérés et ceux-ci doivent correspondre à des permutations circulaires du nombre. Ainsi, le nombre 076923 n'est pas considéré comme cyclique, même si toutes ses permutations circulaires sont des multiples, car ceux-ci ne sont pas successifs :
- 076923 × 1 = 076923
- 076923 × 3 = 230769
- 076923 × 4 = 307692
- 076923 × 9 = 692307
- 076923 × 10 = 769230
- 076923 × 12 = 923076
Cette restriction exclut aussi des cas triviaux tels :
- chiffres répétés, par exemple : 555
- nombres cycliques répétés, par exemple : 142857142857
- chiffres uniques précédés de zéros, par exemple : "005"
Les chiffres uniques peuvent être considérés comme des nombres cycliques triviaux ou dégénérés.
Relation avec les décimales récurrentes
Les nombres cycliques sont liés aux décimales récurrentes des fractions unitaires. En général, pour un nombre cyclique de longueur L, le développement décimal de
- 1/(L + 1)
a une période de L, et répète le nombre cyclique.
Par exemple :
- 1/7 = 0.142857142857…
Les multiples de ces fractions présentent des permutations circulaires :
- 1/7 = 0.142857142857…
- 2/7 = 0.285714285714…
- 3/7 = 0.428571428571…
- 4/7 = 0.571428571428…
- 5/7 = 0.714285714285…
- 6/7 = 0.857142857142…
En contrepartie, si la période du développement décimal de 1/p est
- p − 1,
alors les chiffres répètent un nombre cyclique.
Formes de nombres cycliques
En s'appuyant sur leur relation aux fractions unitaires, on démontre que les nombres cycliques sont de la forme
où b est la base (10 dans le cas du système décimal) et p est un nombre premier ne divisant pas b. Les nombres premiers p qui génèrent des nombre cycliques sont appelés nombres premiers longs.
Par exemple, le cas b = 10, p = 7 donne le nombre cyclique 142857.
Toutes les valeurs de p ne généreront pas forcément un nombre cyclique selon cette formule; par exemple p = 13 donne 076923076923. Ces cas erronés contiendront toujours une ou plusieurs répétition de chiffres.
Les premières valeurs de p pour lesquels cette formule produit un nombre cyclique en notation décimale sont (séquence A001913 dans l'OEIS) :
- 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983 …
Le patron de cette séquence est issu de la théorie algébrique des nombres. Plus spécifiquement, cette séquence est définie comme l'ensemble des nombres premiers p tels que 10 est une racine primitive modulo p. Une conjecture d'Emil Artin [1] postule que cette séquence contiendrait 37.395..% des nombres premiers.
Construction des nombres cycliques
Les nombres cycliques peuvent être construits par l'algorithme suivant :
Soit b la base (10 en base décimale).
Soit p un nombre premier ne divisant pas b.
Soit t = 0.
Soit r = 1.
Soit n = 0.
Répéter ce qui suit :- Soit t = t + 1
- Soit x = r · b
- Soit d = int(x / p)
- Soit r = x mod p
- Soit n = n · b + d
- Si r ≠ 1, répéter.
Si t = p − 1 alors n est un nombre cyclique.
Cette procédure fonctionne en calculant les décimales de 1/p en base b, par division longue. r est le reste à chaque étape et d est la décimale produite.
L'étape
- n = n · b + d
sert uniquement à colliger les chiffres. Pour les ordinateurs incapables d'opérer sur des nombres entiers très grands, les chiffres doivent être exprimés ou conservés autrement.
Il est notable que si t excède p/2, le nombre est forcément cyclique, sans besoin de calculer les chiffres restants.
Propriétés d'un nombre cyclique
- Le produit d'un nombre cyclique avec le nombre premier ayant servi à le générer consiste en une séquence de chiffres 9. 142857 × 7 = 999999.
- L'addition de l'entier correspondant à la première moitié des chiffres d'un nombre cyclique à l'entier correspondant à la seconde moitié de ceux-ci consiste en une séquence de chiffres 9. 142 + 857 = 999.
- Un nombre cyclique est un nombre parasite.
- Un nombre cyclique tronqué après ses n premiers chiffres (non tous nuls) est une approximation par défaut de la fraction 10n/p. Si r est le reste entier de cette division, alors le nombre cyclique peut être produit en commençant par ses n premiers chiffres, puis en additionnant le r x le nombre précédemment additionné et décalé de n rangs vers la droite :
Exemple : pour p=7, le nombre cyclique est 142857142857...
- avec n=1 : 10 = 7 x 1 + 3 (1 = premier chiffre du nombre cyclique, reste r = 3)
- avec n=2 : 100 = 7 x 14 + 2 (14 = 2 premiers chiffres du nombre cyclique, reste r = 2)
- avec n=3 : 1000 = 7 x 142 + 6 (142 = 3 premiers chiffres du nombre cyclique, reste r = 6)
- ...
et on peut écrire :n=1 n=2 n=3 1 x3 14 x2 142 x6 3 | 28 | 852 | 9 v 56 v 5112 v 27 112 30672 81 224 184032 243 448 1104192 + 729 + 896 + 6625152 --------- ---------------- ----------------------- 1428... 14285714285... 1428571428571428...Autres bases
En utilisant la technique décrite plus haut, on peut trouver les nombres cycliques d'autres bases arithmétiques. On doit noter toutefois que toutes les bases ne respectent pas forcément la seconde règle (les multiples successifs doivent tous être des permutations circulaires) indiquée dans la section des cas spéciaux ci-dessus.
En base binaire, la séquence des nombres cycliques commence comme suit :
- 01
- 0011
- 0001011101
- 000100111011
- 000011010111100101
En base ternaire :
- 0121
- 010212
- 0011202122110201
- 001102100221120122
- 0002210102011122200121202111
En base octale :
- 25
- 1463
- 0564272135
- 0215173454106475626043236713
- 0115220717545336140465103476625570602324416373126743
En base duodécimale :
- 2497
- 186A35
- 08579214B36429A7
En base 24 :
- 3A6LDH
- 248HAMKF6D
- 1L795CN3GEJB
- 19M45FCGNE2KJ8B7
Noter qu'en notation ternaire (b = 3), le cas p = 2 génère 1 comme nombre cyclique. Bien que les chiffres uniques puissent être considérés des cas triviaux, il peut être utile, pour la complétude de la théorie, de les considérer, mais uniquement lorsqu'ils sont générés de cette façon.
On peut démontrer qu'aucun nombre cyclique (autre que les chiffres uniques triviaux) d'aucune base arithmétique n'est un carré parfait ; ainsi il n'y a aucun nombre cyclique en base hexadécimale.
Bibliographie
- Gardner, Martin, Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments From Scientific American, New York: The Mathematical Association of America, 1979. pp. 111-122.
- Kalman, Dan, Fractions with Cycling Digit Patterns, The College Mathematics Journal, Vol. 27, No. 2. (Mar., 1996), pp. 109-115.
- Leslie, John, The Philosophy of Arithmetic: Exhibiting a Progressive View of the Theory and Practice of .... Longman, Hurst, Rees, Orme, and Brown, 1820.
- Wells, David, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Press, ISBN 0-14-008029-5
Source
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cyclic number » (voir la liste des auteurs)
Voir aussi
Articles connexes
Liens externes
- (en) Eric W. Weisstein, « Cyclic Number », MathWorld
Catégorie :- Propriété décimale
Wikimedia Foundation. 2010.