Méthode de nelder-mead
- Méthode de nelder-mead
-
Méthode de Nelder-Mead
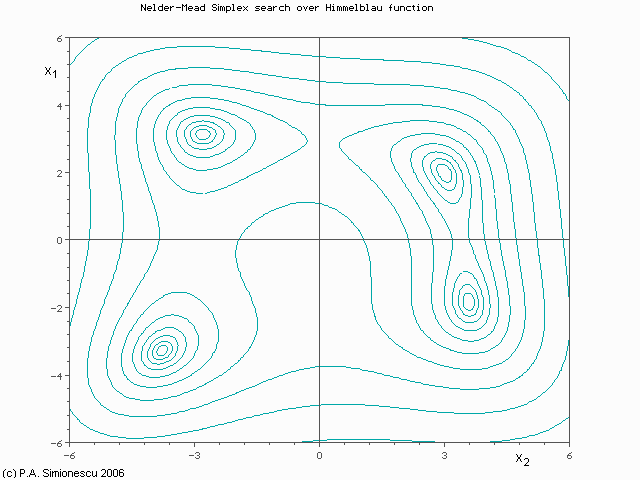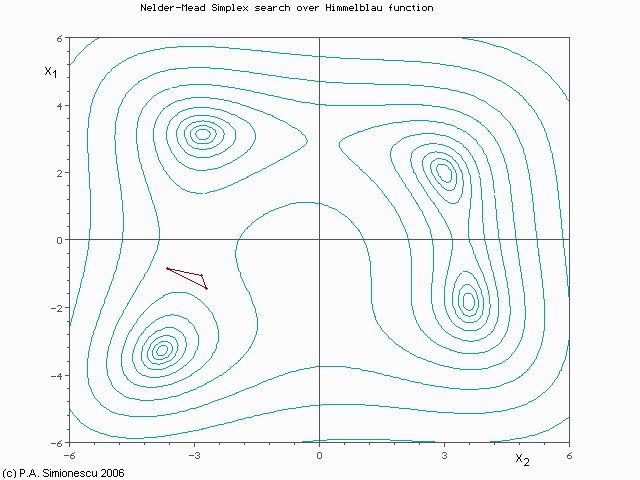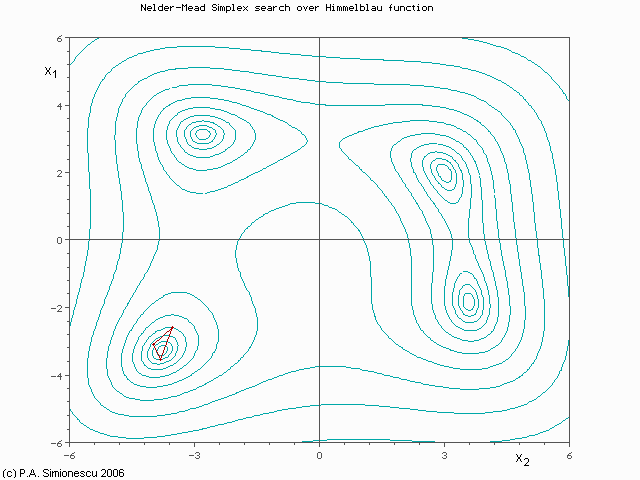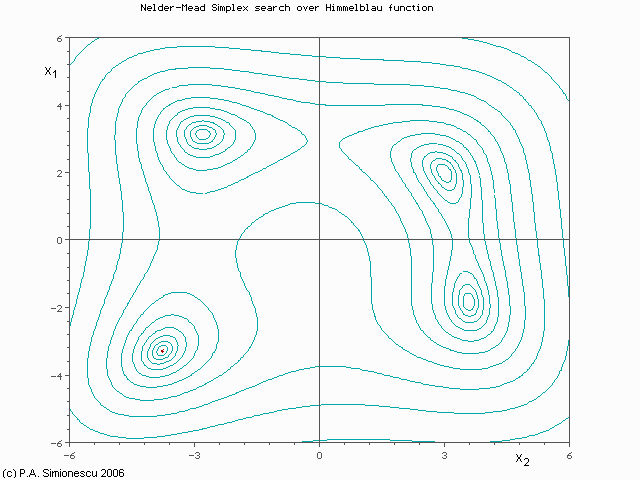
Illustration de la méthode de Nelder-
Mead
La méthode de Nelder-Mead est un algorithme d'optimisation non-linéaire. Elle est publiée[1] par Nelder et Mead en 1965. C'est une méthode numérique qui minimise une fonction dans un espace à plusieurs dimensions.
Cette méthode utilise le concept de simplexe qui est un polytope de N+1 sommets dans un espace à N dimensions.
Soit N la dimension de l'espace où f prend ses valeurs. On démarre avec un simplexe de cet espace. La première étape consiste à enlever le point du simplexe où la fonction est maximale et à le remplacer par la réflexion de ce point par rapport au centre de gravité des N points restants. Si ce point est meilleur, on étire le simplexe dans cette direction. Sinon, on est dans une vallée, et on réduit le simplexe par une similitude centrée sur le point du simplexe où la fonction est minimale.
Algorithme
- Choix de N+1 points de l'espace à N dimensions des inconnues, formant un simplexe : {x1,x2,...,xN + 1},
- Calcul des valeurs de la fonction f en ces points, réindexation des points de façon à avoir
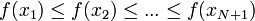 ,
,
- Calcul de x0, centre de gravité de tous les points sauf xN + 1,
- Calcul de xr = x0 + (x0 − xN + 1) (réflexion de xN + 1 par rapport à x0),
- Si f(xr) < f(x1), calcul de xe = x0 + 2(x0 − xN + 1) (étirement du simplexe). Si f(xe) < f(xr), remplacement de xN + 1 par xe, sinon, remplacement de xN + 1 par xr. Retour à l'étape 2.
- Si f(xn) < f(xr), calcul de xc = xN + 1 + 1 / 2(x0 − xN + 1) (contraction du simplexe). Si
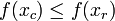 , remplacement de xN + 1 par xc et retour à l'étape 2,
, remplacement de xN + 1 par xc et retour à l'étape 2,
- Similitude de rapport 1/2 et de centre x1 : remplacement de xi par x0 + 1 / 2(xi − x1). Retour à l'étape 2.
Notes et références
- ↑ (en) John Nelder et Roger Mead, « A simplex method for function minimization », dans Computer Journal, vol. 7, no 4, 1965, p. 308-313
Catégorie : Algorithme d'optimisation
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Méthode de nelder-mead de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Methode de Nelder-Mead — Méthode de Nelder Mead Illustration de la méthode de Nelder Mead La méthode de Nelder Mead est un algorithme d optimisation non linéaire. Elle est publiée[1] par Nelder et Mead en 1965. C est une méthode numérique qui minimise une fonction dans… … Wikipédia en Français
Méthode De Nelder-Mead — Illustration de la méthode de Nelder Mead La méthode de Nelder Mead est un algorithme d optimisation non linéaire. Elle est publiée[1] par Nelder et Mead en 1965. C est une méthode numérique qui minimise une fonction dans un espace à plusieurs… … Wikipédia en Français
Méthode de Nelder-Mead — Illustration de la méthode de Nelder Mead sur la fonction de Rosenbrock La méthode de Nelder Mead est un algorithme d optimisation non linéaire. Elle est publiée[1] par Nelder … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Optimisation (mathématiques) — L optimisation est une branche des mathématiques, cherchant à analyser et à résoudre analytiquement ou numériquement les problèmes qui consistent à déterminer le meilleur élément d un ensemble, au sens d un critère quantitatif donné. Ce mot vient … Wikipédia en Français
Algorithme du simplexe — L algorithme du simplexe de George Dantzig est une technique à la fois fondamentale et très populaire pour les problèmes d optimisation linéaire. Ainsi, étant donné un ensemble d inégalités linéaires sur n variables réelles, l algorithme permet… … Wikipédia en Français
Fonction de Rosenbrock — Graphe de la fonction de Rosenbrock La fonction de Rosenbrock est une fonction non convexe de deux variables utilisée comme test pour des problèmes d optimisation mathématique. Elle a été introduite par Rosenbrock en 1960. Elle est aussi connue… … Wikipédia en Français
Downhill-Simplex-Verfahren — Der Simplex Algorithmus nach John Nelder und Roger Mead (Comp. J., vol. 7, 1965, p. 308) oder auch Downhill Simplex Verfahren oder manchmal auch einfach Simplex Algorithmus ist im Unterschied zum Namensvetter für lineare Probleme (Simplex… … Deutsch Wikipedia
Simulationsbasierte Optimierung — Die Idee der simulationsbasierten Optimierung (SBO) besteht darin, mit Simulationsmodellen eine Optimierungskomponente zu verbinden, die bestimmte Variablen eines Simulationsmodells zur Minimierung oder Maximierung einer Zielfunktion variiert.… … Deutsch Wikipedia
Simplex-Verfahren — Das Simplex Verfahren läuft von einer Ecke eines LP Polyeders zur nächsten, bis keine Verbesserung mehr möglich ist. Das Simplex Verfahren (auch Simplex Algorithmus) ist ein Optimierungsverfahren der Numerik zur Lösung linearer… … Deutsch Wikipedia
 Illustration de la méthode de Nelder-Mead
Illustration de la méthode de Nelder-Mead
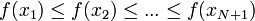 ,
,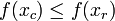 , remplacement de xN + 1 par xc et retour à l'étape 2,
, remplacement de xN + 1 par xc et retour à l'étape 2,