- Méthode De Crank-Nicolson
-
Méthode de Crank-Nicolson
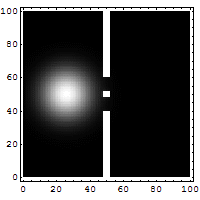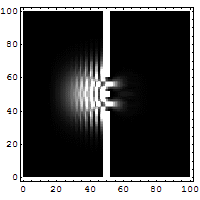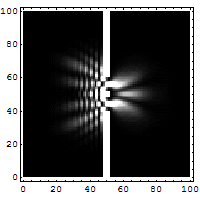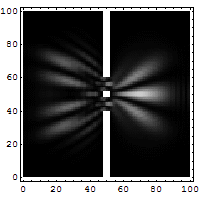Simulation de l'expérience des fentes de Young pour un électron, avec la méthode de Crank-Nicolson.En mathématiques, en analyse numérique, la méthode de Crank-Nicolson est un algorithme simple permettant de résoudre des systèmes d'équations aux dérivées partielles. Cette méthode utilise les différences finies pour approcher une solution du problème : elle est numériquement stable[1],[2] et quadratique pour le temps. On peut facilement la généraliser à des problèmes à deux ou trois dimensions.[3]
Cette méthode, publiée en 1947, est le résultat des travaux de la mathématicienne britannique Phyllis Nicolson[4] (1917 — 1968) et du physicien John Crank[5] (1916 — 2006). Ils l'utilisèrent dans la résolution de l'équation de la chaleur. [6]
Son efficacité et sa simplicité en font un outil courant dans les simulations numériques, pour résoudre des problèmes de mécanique quantique, de thermodynamique hors-équilibre[7],[8], de mécanique des fluides[9] et d'électromagnétisme[10]. Par ailleurs, un certain nombre de phénomènes pouvant être ramenés à l'étude de l'équation de la chaleur, son champ d'application est relativement étendu : à partir du modèle Black-Scholes, on peut par exemple utiliser la méthode de Crank-Nicolson à la finance.
Sommaire
Principes
On peut comprendre la méthode de Crank-Nicolson comme la moyenne temporelle de ce que donne la méthode d'Euler progressive et de la méthode d'Euler régressive. Elle consiste à intégrer dans le temps par la méthode des trapèzes et à utiliser les différences finies dans l'espace.
Cette méthode est inconditionnellement stable, mais nécessite certaines conditions de régularité sur les équations à résoudre pour que le résultat ait une précision satisfaisante.[2]
Voir aussi
Notes et références
- ↑ (fr) Comparaison de la stabilité de différentes méthodes d'intégration numérique, Université catholique de Louvain.
- ↑ a et b (fr) Les espaces de Sobolev, Université de Liège.
- ↑ (en) « The alternating segment difference scheme for Burgers' equation», Shandong University, 2005. ISSN 0271-2091.
- ↑ (en) Biographie : Phyllis Nicolson.
- ↑ (en) Biographie : Jonh Crank.
- ↑ (en) J.Crank, P.Nicolson : « A practical method for numerical evaluation of solutions of partial differential equations of the heat conduction type », Proceedings of the Cambridge Philosophical Society, 1947.
- ↑ (en) Résolution de l'équation de la chaleur par la méthode de Crank-Nicolson, Université d'État de Californie à Fullerton.
- ↑ (en) Simulation d'une interface thermique par la méthode de Crank-Nicolson.
- ↑ (fr) d'un écoulement incompressible, étudié par la méthode de Crank-Nicolson.
- ↑ (en) Résolution des équations de Maxwell par la méthode de Crank-Nicolson, INRIA.
Bibliographie
- (en) P. Wilmott, S. Howison, J. Dewynne « The Mathematics of Financial Derivatives : A Student Introduction », Cambridge University Press, 1995.
Portail de la physique
Catégories : Équations différentielles numériques | Algorithme
Wikimedia Foundation. 2010.
