Algorithme De Karatsuba

L'algorithme de Karatsuba (1960) est une méthode permettant de multiplier rapidement deux nombres avec une complexité en 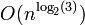au lieu de O(n²) pour la méthode naïve. Note : .

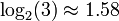Sommaire 1 Énoncé 2 Exemple 3 References 4 Voir aussi

Énoncé

Pour multiplier deux nombres de n chiffres, la méthode naïve multiplie chaque chiffre du multiplicateur par chaque chiffre du multiplicande. Cela exige donc n² produits de deux chiffres. Le temps de calcul est en O(n²).

En 1960, Karatsuba remarque que le calcul de (a × 10^k + b)(c × 10^k + d) qui, sous forme développée ac × 10^2k + (ad + bc) × 10^k + bd, semble nécessiter les quatre produits ac, ad, bc et bd, peut en fait être effectué seulement avec les trois produits ac, bd et (a – b)(c – d) en regroupant les calculs sous la forme suivante :

(a × 10^k + b)(c × 10^k + d) = ac × 10^2k + (ac + bd – (a – b)(c – d)) × 10^k + bd

Ainsi, pour calculer 26 × 34, on calcule

2 × 3 = 6

6 × 4 = 24

(2 – 6) × (3 – 4) = 4

Le résultat final est alors 6 × 100 + (6 + 24 – 4) × 10 + 24 = 600 + 260 + 24 = 884. La multiplication par la base de numération (10 dans l'exemple précédent mais en binaire pour les machines) qui correspond à un décalage de chiffre, et les additions sont peu coûteuses en temps. Pour de grands nombres, la méthode peut être appliquée de manière récursive pour les calculs de ac, bd et (a – b)(c – d) en scindant à nouveau a, b, c et d en deux et ainsi de suite.

Exemple

Ainsi, 12378456 × 25874215 est calculé, en prenant une base 10000, comme suit :

1237 × 2587

8456 × 4215

(1237 – 8456) × (2587 – 4215) = 7219 × 1628

Le produit 1237 × 2587 est lui-même calculé, en prenant une base 100, comme suit :

12 × 25

37 × 87

(12 – 37) × (25 – 87) = 25 × 62

Le produit 12 × 25 est calculé, en prenant une base 10, au moyen de :

1 × 2 = 2

2 × 5 = 10

(1 – 2) × (2 – 5) = 1 × 3 = 3

pour obtenir 12 × 25 = 2 × 100 + (2 + 10 – 3) × 10 + 10 = 300. On obtient de même :

12 × 25 = 300

37 × 87 = 3219

25 × 62 = 1550

d'où 1237 × 2587 = 300 × 100² + (300 + 3219 – 1550) × 100 + 3219 = 3000000 + 196900 + 3219 = 3200119. On procède de même pour les produits 8456 × 4215 et 7219 × 1628, obtenant finalement :

1237 × 2587 = 3200119

8456 × 4215 = 35642040

7219 × 1628 = 11752532

D'où, enfin : 12378456 × 25874215 = 3200119 × 10000² + (3200119 + 35642040 – 11752532) × 10000 + 35652040

= 320011900000000 + 270896270000 + 35642040

= 320282831912040

Le calcul complet ne demande que 27 produits de deux chiffres au lieu de 64 par la méthode usuelle. Bien entendu, cette méthode, fastidieuse à la main, révèle toute sa puissance pour une machine devant effectuer le produit de grands nombres. On obtient alors un algorithme dit de multiplication rapide de deux nombres de n chiffres en 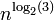opérations élémentaires (tels que produit ou somme de deux chiffres) au lieu de n². Pour n = 1000, 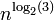est de l'ordre de 50 000 alors que n² = 1 000 000.

Toom et Cook améliorèrent cette méthode en découpant les nombres en r blocs (au lieu de 2). Le temps de calcul en O(n²) par la méthode naïve passe alors en O(n^1+ε) où ε est un réel positif arbitraire.

References

• A. Karatsuba and Yu Ofman, Multiplication of Many-Digital Numbers by Automatic Computers. Doklady Akad. Nauk SSSR Vol. 145 (1962), pp. 293–294. Translation in Physics-Doklady 7 (1963), pp. 595–596.
• Karacuba A. A. Berechnungen und die Kompliziertheit von Beziehungen (German) // Elektron. Inform.-verarb. Kybernetik, 11, 603–606 (1975).
• Karatsuba A. A. The complexity of computations // Proc. Steklov Inst. Math., 211, 169–183 (1995); translation from Trudy Mat. Inst. Steklova, 211, 186–202 (1995).
• Knuth D. E. The art of computer programming. v.2. Addison-Wesley Publ.Co., 724 pp., Reading (1969).
• Karatsuba Multiplication on Fast Algorithms and the FEE

Voir aussi

• Technique de multiplication
• Algorithme Toom-Cook
• Anatolii Alexevich Karatsuba

Algorithmes de multiplication
Produit de matrices	Naïf  · Strassen  · Coppersmith-Winograd
Produit d'entiers	Naïf  · Karatsuba  · Toom-Cook  · Schönhage-Strassen  · Fürer

• Portail des mathématiques