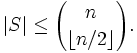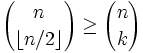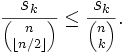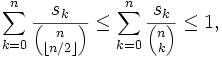Famille de sperner

Famille de Sperner

En combinatoire, une famille de Sperner (ou système de Sperner), appelé en l'honneur d'Emanuel Sperner, est système d'ensembles (F, E) dans lequel aucun élément ne contient un autre. Formellement,

Si X, Y sont dans F et X ≠ Y, alors X n'est pas contenu dans Y et Y n'est pas contenu dans X.

De manière équivalente, une famille de Sperner est une antichaîne sur des treillis inclus sans des puissance cartésienne de E.

Théorème de Sperner

Pour toute famille de Sperner S sur un ensemble à n éléments

$|S| \le {n \choose \lfloor{n/2}\rfloor}.$

Preuve

Cette preuve est due à Lubell. Soit s_k le nombre d'ensemble à k éléments de S. Pour tout 0 ≤ k ≤ n,

${n \choose \lfloor{n/2}\rfloor} \ge {n \choose k}$

et donc,

${s_k \over {n \choose \lfloor{n/2}\rfloor}} \le {s_k \over {n \choose k}}.$

Comme S est une antichaine, on peut sommer les précédentes inégalités de k=0 à n et ensuite appliquer ingalité de Lubell-Yamamoto-Meshalkin pour obtenir

$\sum_{k=0}^n{s_k \over {n \choose \lfloor{n/2}\rfloor}} \le \sum_{k=0}^n{s_k \over {n \choose k}} \le 1,$

ce qui s'écrit

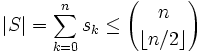$|S| = \sum_{k=0}^n s_k \le {n \choose \lfloor{n/2}\rfloor}$ .

Ce qui termine la preuve.

Le théorème de Sperner peut être vu comme un cas spécial du théorème Dilworth. Il est parfois appelé à tort Lemme de Sperner, car ceci fait référence à un autre résultat de combinatoire sur la coloration de graphe.

Références

Lubell, D. (1966). A short proof of Sperner's theorem, J. Combin. Theory 1, 299.

Portail des mathématiques

Ce document provient de « Famille de Sperner ».

Catégorie : Analyse combinatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Famille de sperner de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Famille De Sperner — En combinatoire, une famille de Sperner (ou système de Sperner), appelé en l honneur d Emanuel Sperner, est système d ensembles (F, E) dans lequel aucun élément ne contient un autre. Formellement, Si X, Y sont dans F et X ≠ Y, alors X n est pas… … Wikipédia en Français
Famille de Sperner — En combinatoire, une famille de Sperner (ou système de Sperner), appelé en l honneur d Emanuel Sperner, est un hypergraphe (E, F) (c est à dire un ensemble E et un ensemble F de parties de E) dans lequel aucun élément de F ne contient un autre.… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Hypergraphe — Exemple d hypergraphe : V = {v1,v2,v3,v4,v5,v6,v7}, E = {e1,e2,e3,e4} = {{v1,v2,v3},{v2,v3}, {v3,v … Wikipédia en Français
Hypergraphes — Hypergraphe Exemple d hypergraphe: V = {v1,v2,v3,v4,v5,v6,v7}, E = {e1,e2,e3,e4} = {{v1,v2,v3},{v2,v3}, {v3,v5,v6},{v4}}. Les hyperg … Wikipédia en Français
Antichaîne — En mathématiques, plus précisément en théorie des ordres, une antichaîne d un ensemble E muni d une relation d ordre (notée ici ≤ ) est une partie A de E telle que Autrement dit, dans un ensemble ordonné, une antichaîne est une partie dont les… … Wikipédia en Français
Théorème du point fixe de Brouwer — En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Famille de sperner