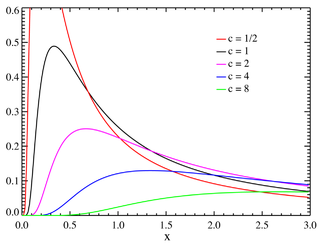
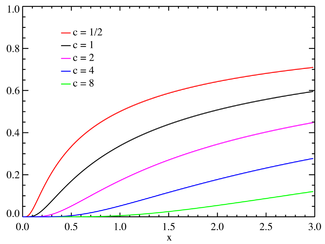
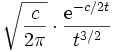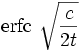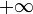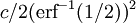Loi de Lévy
Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Lévy de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Loi De Lévy — Distribution de Lévy Distribution de Lévy Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi de Levy — Distribution de Lévy Distribution de Lévy Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi de lévy — Distribution de Lévy Distribution de Lévy Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi Normale — Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi Normale Reduite — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi de Gauss — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi de Laplace-Gauss — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi normale gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
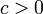
![t \in ]0, +\infty[\,](/pictures/frwiki/48/0703abc4c995a6b0c9b720ed541c462f.png)