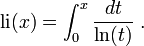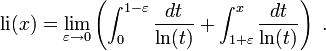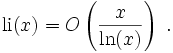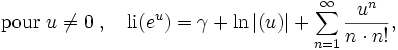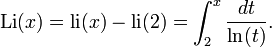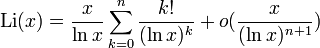Logarithme integral

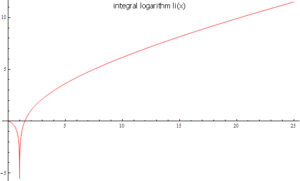
Logarithme integral

Logarithme intégral

Logarithme intégral

En mathématiques, le logarithme intégral li est une fonction spéciale définie en tout nombre réel strictement positif x≠1 par l'intégrale :

{\rm li} (x) = \int_{0}^{x} \frac{dt}{\ln (t)} \;.

Ici, ln désigne le logarithme naturel. La fonction 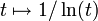t\mapsto 1/\ln (t) n'est pas définie en t = 1, et l'intégrale pour x> 1 doit être interprétée comme la valeur principale de Cauchy :

{\rm li} (x) = \lim_{\varepsilon \to 0} \left( \int_{0}^{1-\varepsilon} \frac{dt}{\ln (t)} + \int_{1+\varepsilon}^{x} \frac{dt}{\ln (t)} \right) \;.

Le comportement de croissance de cette fonction pour x → ∞ est

{\rm li} (x) = O \left( {x\over \ln (x)} \right) \;.

(Voir Notation O).

La fonction li est liée à l'exponentielle intégrale Ei par la relation li(x) = Ei (ln (x)) pour tout nombre réel strictement positif x ≠ 1. Ceci mène aux développements en séries de li (x), comme par exemple:

{\rm pour} \; u \ne 0 \;,\quad {\rm li} (e^{u}) = \gamma + \ln \left| (u) \right| + \sum_{n=1}^{\infty} {u^{n}\over n \cdot n!},

où γ ≈ 0.57721 56649 01532... est la constante d'Euler-Mascheroni.

La fonction li a une seule racine, elle se trouve en x ≈ 1.45136 92348...; ce nombre est connu comme étant la constante de Ramanujan-Soldner.

Fonction d'écart logarithmique intégrale

La fonction d'écart logarithmique intégrale est une fonction spéciale Li(x) très similaire à la fonction logarithme intégral, définie de la façon suivante :

\mathrm{Li}(x) = \mathrm{li}(x) - \mathrm{li}(2)=\int_{2}^{x} \frac{dt}{\ln (t)}.

Il peut être montré que, pour tout entier n, on a le développement asymptotique suivant à l'infini :

{\rm Li} (x) = \frac{x}{\ln x} \sum_{k=0}^{n} \frac{k!}{(\ln x)^k} + o(\frac{x}{(\ln x)^{n+1}})

Elle est souvent utilisée dans les formulations du théorème des nombres premiers. L'écart logarithmique intégral donne une légèrement meilleure estimation de la fonction de compte des nombres premiers que la fonction li.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Logarithme int%C3%A9gral ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Logarithme integral de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Logarithme Intégral — En mathématiques, le logarithme intégral li est une fonction spéciale définie en tout nombre réel strictement positif x≠1 par l intégrale  …   Wikipédia en Français

  • Logarithme intégral — En mathématiques, le logarithme intégral li est une fonction spéciale définie en tout nombre réel strictement positif x≠1 par l intégrale : Ici, ln désigne le …   Wikipédia en Français

  • logarithme intégral — integralinis logaritmas statusas T sritis fizika atitikmenys: angl. integral logarithm vok. Integrallogarithmus, m rus. интегральный логарифм, m pranc. logarithme intégral, m …   Fizikos terminų žodynas

  • Logarithme Naturel — Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en 1. Le logarithme… …   Wikipédia en Français

  • Logarithme Népérien — Logarithme naturel Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en… …   Wikipédia en Français

  • Logarithme naturel — Le logarithme naturel ou logarithme népérien est, en mathématiques, la fonction logarithme de base e. C est donc la réciproque de la fonction exponentielle de base e. C est aussi la primitive définie sur ] 0 , + ∞ [ et qui s annule en 1 de la… …   Wikipédia en Français

  • Logarithme népérien — Logarithme naturel Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en… …   Wikipédia en Français

  • integral logarithm — integralinis logaritmas statusas T sritis fizika atitikmenys: angl. integral logarithm vok. Integrallogarithmus, m rus. интегральный логарифм, m pranc. logarithme intégral, m …   Fizikos terminų žodynas

  • Fonction logarithme (mathématiques élémentaires) — Logarithme naturel Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en… …   Wikipédia en Français

  • Sinus intégral —  Ne pas confondre avec la fonction sinus cardinal. Tracé de Si(x) pour . La fo …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”