Limite Inductive

Limite inductive

En mathématiques, la notion de limite inductive (parfois appelée limite directe, suivant l'anglais direct limit) est utilisée pour considérer simultanément toute une famille d'objets, par exemple des groupes, liés entre eux par une famille de morphismes, par exemple des morphismes de groupes. Cette notion est duale de celle de limite projective.

Le cadre général pour cette notion est celui des catégories.

Définition concrète

Pour fixer les idées, on parle d'abord de limite inductive d'ensembles.

On considère une famille (A_i)_i∈I d'ensembles, indexée par un ensemble I ordonné, et munie d'une famille d'applications f_ij : A_i → A_j pour tout i ≤ j (remarquer l'ordre : du plus petit indice i vers le plus grand j, au contraire d'une limite projective) vérifiant les conditions de compatibilité :

f_ii est l'identité sur A_i,
f_ik = f_jk O f_ij pour tous i ≤ j ≤ k.

La donnée (I, A_i, f_ij) est appelée système inductif d'ensembles. La limite inductive de ce système, notée 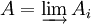$A=\varinjlim A_i$ est alors définie comme le quotient de l'union disjointe des ensembles A_i, par la relation d'équivalence :

$\{x_i\in A_i \sim x_j\in A_j \mid \mbox{ il existe } k\geq i,j \mbox{ tel que } f_{ik}(x_i) = f_{jk}(x_j)\}$

On en déduit des applications naturelles φ_i : A_i → A, envoyant chaque élément sur sa classe d'équivalence.

Définir la limite directe pour une structure plus forte demande de disposer d'une généralisation adaptée de la notion d'union disjointe ; le produit libre pour les groupes convient par exemple.

Définition par propriété universelle

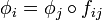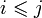Soit (X_i, f_ij) un système inductif dans une catégorie C (la définition donnée ci-dessus pour les ensembles s'adapte à n'importe quelle catégorie). La limite inductive X est un objet de la catégorie C muni de flèches $φ i$ de X_i à valeurs dans X vérifiant les relations de compatibilité $\phi_i=\phi_j\circ f_{ij}$ pour tous $i\leqslant j$ . De plus, la donnée $(X,φ i)$ doit être universelle : pour tout autre objet Y muni d'une famille de flèches ψ_i il existe une unique flèche u : Y → X telle que le diagramme :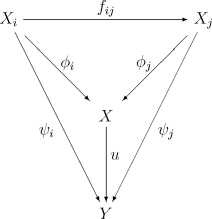

soit commutatif pour tous i ≤ j. La limite inductive est notée : 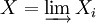$X = \varinjlim X_i$ . On parlera de limite inductive des X_i suivant les morphismes de transition f_ij, ou par abus de langage, de limite suivant I, voir tout simplement de limite inductive des X_i.

Contrairement au cas concret de la catégorie des ensembles, où la définition comme quotient de l'union disjointe assure l'existence d'une limite inductive, la limite inductive peut ne pas exister dans une catégorie générale. En revanche, l'unicité si existence est toujours assurée : si X′ est une autre limite inductive, il existe un unique isomorphisme X′ → X qui commute avec les morphismes φ_i.

Exemple

Soit p un nombre premier. Pour tout n soit U_n le groupe cyclique des racines pⁿ-ièmes de l'unité dans un corps algébriquement clos. On considère les inclusions comme morphismes de transition. La limite directe de ce système est alors le groupe infini constitué de toutes les racines p-primaires de l'unité.

Portail des mathématiques

Ce document provient de « Limite inductive ».

Catégorie : Théorie des catégories

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Limite Inductive de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Limite inductive — Sommaire 1 Avant propos 2 Ensemble ordonné filtrant 3 Système inductif 4 Propriété universelle de la limite inductive … Wikipédia en Français
Limite Projective — En mathématiques, la notion de limite projective (inverse limit en anglais) est utilisée pour considérer simultanément toute une famille d objets, par exemple des groupes, liés entre eux par une famille de morphismes, par exemple des morphismes… … Wikipédia en Français
Limite projective — En mathématiques, formalisée dans le langage des catégories, la limite projective est une généralisation du produit. Cette notion est duale de celle de limite inductive. Sommaire 1 Limite projective d ensembles 2 Système projectif … Wikipédia en Français
Inférence inductive — Induction (logique) Pour les articles homonymes, voir Induction. À la différence de la déduction qui impose des propositions de départ non supposées vraies, l induction se propose de chercher des lois générales à partir de l observation de faits… … Wikipédia en Français
Recherche inductive — Induction (logique) Pour les articles homonymes, voir Induction. À la différence de la déduction qui impose des propositions de départ non supposées vraies, l induction se propose de chercher des lois générales à partir de l observation de faits… … Wikipédia en Français
TOPOLOGIQUES (ESPACES VECTORIELS) — La théorie des espaces normés, développée par S. Banach et ses élèves, s’est vite révélée insuffisante pour les besoins de l’analyse fonctionnelle où interviennent de nombreux espaces vectoriels munis d’une topologie qui n’est pas déduite d’une… … Encyclopédie Universelle
Préfaisceau — En mathématiques, et plus particulièrement dans la théorie des catégories, un préfaisceau sur un espace topologique X est un foncteur contravariant de la catégorie des ouverts de X dans une autre catégorie. On peut donc avoir des préfaisceaux d… … Wikipédia en Français
Prefaisceau — Préfaisceau En mathématiques, et plus particulièrement dans la théorie des catégories, un préfaisceau sur un espace topologique X est un foncteur contravariant de la catégorie des ouverts de X dans une autre catégorie. On peut donc avoir des… … Wikipédia en Français
CATÉGORIES ET FONCTEURS — Introduite en 1945 par Eilenberg et MacLane pour rendre compte de propriétés très générales des structures mathématiques, la théorie des catégories a quelque peu pâti, à ses débuts, de cette généralité qui lui valut auprès des «mathématiciens… … Encyclopédie Universelle
NORMÉES (ALGÈBRES) — Au point de rencontre de deux types de structures, structures algébriques et structures topologiques, les algèbres normées jouent un rôle important dans de nombreux domaines de l’analyse mathématique. Développée à partir de 1940 environ,… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Limite Inductive