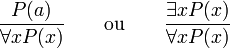Recherche inductive

À la différence de la déduction qui impose des propositions de départ non supposées vraies, l'induction se propose de chercher des lois générales à partir de l'observation de faits particuliers, sur une base probabiliste.

L'idée de départ de l'induction était que la répétition d'un phénomène en augmente la probabilité de le voir se reproduire. C'est là proprement la façon dont réagit le cerveau chez le chien de Pavlov par exemple. L'accumulation de faits concordants et l'absence de contre-exemples permet ensuite d'augmenter le niveau de plausibilité de la loi jusqu'au moment où on choisit par simplification de la considérer comme une quasi certitude : ainsi en est-il du deuxième principe de la thermodynamique. En aucun cas, cependant, on n'atteindra la certitude, tout contre exemple étant susceptible de remettre immédiatement cette "loi" en cause.

Par la suite, des théorèmes comme celui de Cox donneront à cette démarche inductive empirique une base mathématique ferme, et permettra de calculer les probabilités concernées sans aucun arbitraire à une position de départ près.

Remarque: Bien qu'associée dans le titre à la logique, la présentation qui suit correspond à la notion « philosophique » de l'induction. En effet, en mathématiques, en logique et en informatique, l'induction complète, aujourd'hui très souvent abrégée en induction, est une autre façon de désigner la récurrence : aussi bien le raisonnement par récurrence que les définitions par récurrence. Le terme est souvent employé pour les généralisations de la récurrence aux bons ordres et relations bien fondées. En raisonnement automatisé, l'abduction est un mode de raisonnement qui vise à émettre une hypothèse pour expliquer un fait et ne doit pas être confondue avec l'induction présentée ici^[1].

Sommaire 1 Exemple 2 Ancienne vision de l'induction 3 Quelques exemples classiques 4 L'induction sous forme d'une règle formelle de raisonnement 5 Notes et références 6 Voir aussi 6.1 Articles connexes 6.2 Liens externes 6.3 Bibliographie

Exemple

Par exemple : Si la loi de la gravitation universelle détermine que, et comment, une pomme qui se détache de son arbre tombera sur le sol, l'observation du mouvement de cette même pomme permet d'établir la loi générale, mais avec une probabilité ou une certitude très faible. Si ensuite, on observe que toutes les pommes et tous les corps tombent de la même façon, si on observe que les corps dans l'espace respectent la même loi, alors la probabilité de la loi augmentera jusqu'à devenir une quasi certitude. Dans le cas de la gravitation universelle, cependant, on a observé que l'orbite de Mercure présentait un effet de précession qui n'était pas expliqué par la loi^[2]. La loi de la gravitation universelle est cependant restée utilisée jusqu'à ce qu'Einstein propose la théorie de la relativité générale qui, elle, explique le phénomène. Malgré tout, la gravitation universelle reste utilisée car elle reste valable dans les cas courants, et elle est plus simple à utiliser et à comprendre que la théorie de la relativité.

Ancienne vision de l'induction

De manière générale, l'induction, contrairement à la déduction, est un raisonnement logiquement inexact, qui est appuyé par sa vérification répétée, mais qui peut être démenti par un contre-exemple. Il est cependant universellement utilisé pour deux raisons :

• À l'exclusion de la logique et des mathématiques qui consistent explicitement à poser des axiomes arbitraires sur base desquels elles raisonnent par la déduction, toutes les autres sciences tentent de décrire la réalité et ne peuvent le faire qu'exclusivement sur base de la vérification par l'observation, ce qui les force à faire appel à l'induction et leur interdit toute possibilité d'utiliser la déduction pure.
• Tous les systèmes vivants fonctionnent sur base de l'induction. L'apprentissage par le cerveau se basant sur sa confrontation avec la réalité, est essentiellement inductif, et, par extension, en intelligence artificielle, les systèmes d'apprentissage à réseau de neurones se différencient des systèmes algorithmiques en ce qu'ils sont inductifs, alors que les systèmes algorithmiques sont déductifs. La sélection naturelle, elle même, en éliminant les plus faibles par la confrontation de l'espèce avec les difficultés de l'existence, est aussi un phénomène fondamentalement inductif.

Note: il est assez curieux d'observer que le principe de déduction est infiniment plus simple que le principe d'induction, pourtant, la vie s'adapte selon le principe d'induction et, paradoxalement, le cerveau qui est conçu pour l'induction n'est pas une machine logique : il n'intègre pas spontanément et doit acquérir la déduction qui est pourtant plus simple.

Il faut remarquer que si l'induction est un raisonnement intrinsèquement probabiliste, il est cependant impossible d'évaluer la probabilité sous-jacente. En effet, celle ci est une probabilité conditionnelle et restera toujours soumise aux choix des conditions de son évaluation, sachant qu'il peut y avoir des conditions auxquelles on n'a pas pensé et qui changeraient complètement les données du problème.

exemple : Si je ne rencontre que des chats gris, il me sera facile d'en induire que tous les chats sont gris avec un fort niveau de certitude. Mais si je réalise que le fait que les chats sont gris pourrait être spécifique à la région ou je vis, et qu'il pourrait exister une autre région ou tous les chats sont roux et encore une autre avec des chats verts (pour prendre une hypothèse réelle ET une hypothèse absurde), mon évaluation de ce niveau de certitude en sera complètement mise en cause.

De plus, le niveau de certitude de ma loi dépendra du coefficient avec lequel j'accepte qu'elle ne soit pas tout à fait générale et admette des exceptions.

Je peux considérer, par exemple, que la relativité générale, est un cas particulier qui ne s'applique que dans des situations réelles, mais que cela ne met pas en cause en général la théorie de la gravitation universelle, ou au contraire, je peux décider que la gravitation universelle doit être précise et exacte, auquel cas, elle est fausse.

Quelques exemples classiques

La plus célèbre des inductions est probablement l'exemple qu'en donne Aristote :

L'âne, le mulet, le cheval vivent longtemps  ;

or, ce sont là tous les animaux sans fiel  ;

donc, tous les animaux sans fiel vivent longtemps.

On voit bien que l'induction repose sur une supposition : que « ce sont là tous les animaux sans fiel ». Le syllogisme inductif est dit hypothétique (non-scientifique) :

Socrate est chauve ;

Socrate est un homme ;

donc les hommes sont chauves.

a une conclusion fausse, car Socrate ne peut pas représenter l'homme, en la matière.

Un exemple célèbre d'induction de Claude Bernard, illustrant la méthode scientifique :

un lapin normalement nourri a une urine basique ;

le même lapin à jeun a une urine acide ;

donc tous les herbivores ont une urine basique ;

alors que tous les animaux mal nourris et les carnivores ont une urine acide.

On voit là l'usage de l'induction : à partir d'observations (qui sont toujours des propositions particulières), l'induction produit des propositions générales hypothétiques qui sont ensuite testables. C'est l'analyse de Claude Bernard, ainsi que celle de Karl Popper.

Hume considérait (Enquête sur l'entendement humain, VII,2) que l'origine de l'induction (l'idée de connexion) est l'habitude. Si cette habitude produit une croyance en l'induction reposant sur une force psychologique, l'induction conserve cependant pour lui une dimension logique très importante puisque Hume établit dans le Traité de la nature humaine les règles de l'induction valide. L'induction a ainsi sa source dans la psychologie humaine, mais sa validité ne s'y réduit pas.

Karl Popper (Conjectures et réfutations, p. 78) soutient au contraire que « Hume [n'a] jamais reconnu toute la portée de sa propre analyse logique », et propose un renversement : « au lieu d'expliquer notre propension à présumer l'existence de régularité comme un effet de la répétition, j'ai imaginé d'expliquer ce qui est répétition à nos yeux comme le résultat de notre tendance à supposer et à rechercher de la régularité ». Mais Hume ne dit pas autre chose : nous sommes en effet selon lui disposés par l'imagination à trouver de la régularité dans les phénomènes. Sans cette disposition, aucune répétition ne produirait en nous de raisonnement inductif.

Longtemps purement empirique, le processus d'induction a été formalisé par le Théorème de Cox-Jaynes qui confirme la rationalité de la méthode pour la mise à jour des connaissances, la quantifie, et unifie l'univers de la logique booléenne avec celui des probabilités (vues non plus en tant que passage à la limite de fréquences, mais comme traduction numérique d'un état de connaissance dans ce paradigme).

L'induction sous forme d'une règle formelle de raisonnement

Pour comprendre l'induction on peut la mettre sous forme d'une règle de raisonnement à la manière de celle de la déduction naturelle. Deux règles sont possibles:

autrement dit « si j'ai démontré ou je constate une^[3] instance P(a) du prédicat P ou si je sais qu'il existe un x qui satisfait P, j'en infère que le prédicat est vrai pour toutes les instances ». Clairement cette règle n'est pas une règle de déduction valide en logique mathématique^[4].

Notes et références

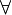Voir aussi

Articles connexes

• Empirisme | Syllogisme
• Raisonnement
• Déduction logique (antonyme)
• Démarche expérimentale
• Biais cognitif (exemple : biais de confirmation d'hypothèse),
• Méthode des concordances
• Concepts logiques
• Déduction et induction

Liens externes

• Frédéric Fabre Réfutation de l'induction probabiliste et corroboration

Bibliographie

• (en)Michael R. Genesereth and Nils J. Nilsson, Logical Foundations of Artificial Intelligence, 1987 [détail des éditions] , chap. 7 Induction, pp. 161-176

• Portail de la logique
• Portail de la philosophie
• Portail des mathématiques