- Analyse discriminante
-
L’analyse factorielle discriminante ou analyse discriminante est une technique statistique qui vise à décrire, expliquer et prédire l’appartenance à des groupes prédéfinis (classes, modalités de la variable à prédire, …) d’un ensemble d’observations (individus, exemples, …) à partir d’une série de variables prédictives (descripteurs, variables exogènes, …).
L’analyse discriminante est utilisée dans de nombreux domaines :
- En médecine, par exemple pour détecter les groupes à hauts risques cardiaques à partir de caractéristiques telles que l’alimentation, le fait de fumer ou pas, les antécédents familiaux, etc.
- Dans le domaine bancaire, lorsque l’on veut évaluer la fiabilité d’un demandeur de crédit à partir de ses revenus, du nombre de personnes à charge, des encours de crédits qu’il détient, etc.
- En biologie, lorsque l’on veut affecter un objet à sa famille d’appartenance à partir de ses caractéristiques physiques. Les iris de Sir Ronald Fisher -- qui est à l'origine de cette méthode—en est un exemple très fameux, il s’agit de reconnaître le type d’iris (setosa, virginica, et versicolor) à partir de la longueur/largeur de ses pétales et sépales.
- En informatique, pour la Reconnaissance optique de caractères. L'analyse discriminante est utilisée pour reconnaître un caractère imprimé à partir d'informations simples, comme la présence ou non de symétrie, le nombre d'extrémités…
L’analyse discriminante est une technique connue et reconnue, elle est décrite à peu près de manière identique par les différentes communautés du traitement de données : en statistique exploratoire (exploratory data analysis), en analyse des données, en reconnaissance de formes (pattern recognition), en apprentissage automatique (machine learning), en fouille de données (data mining), …
Sommaire
Tableau de données
Dans le fichier Flea Beetles Dataset, référencé sur le site DASL (Data and Story Library), nous observons 3 familles de puces caractérisées par l’angle et la largeur de leur édéage, l'organe de reproduction mâle en entomologie.
Nous disposons de 74 observations dans ce fichier. La variable Species indique la famille d’appartenance de chaque puce, il en existe trois {Con – Concinna, Hei – Heikertingeri, Hep - Heptapotamica}. Les puces sont décrites à l’aide de deux variables continues : la largeur (width) et l’angle (angle) de leur aedeagus.
Les données étant décrites par deux variables, il est possible de représenter le nuage de points dans un graphique XY avec en abscisse la largeur (width) et en ordonnée l’angle (angle). Ça n’est plus possible lorsque le nombre de descripteurs est supérieur à deux, un des rôles de l’analyse discriminante est justement de proposer une représentation graphique appropriée dans un espace réduit.
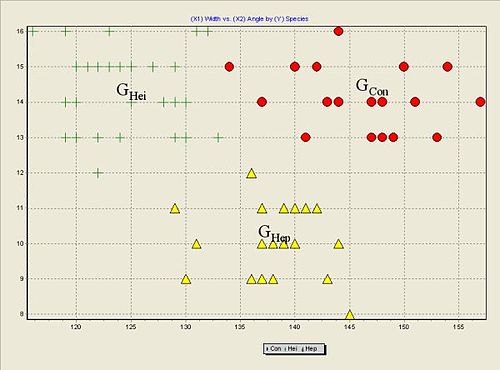 Représentation graphique des données du fichier Flea Beetles Dataset. Nous distinguons bien les trois « blocs » associés à chaque espèce de puce. À chaque nuage de points conditionnel correspond un centre de gravité conditionnel matérialisé par la lettre G.
Représentation graphique des données du fichier Flea Beetles Dataset. Nous distinguons bien les trois « blocs » associés à chaque espèce de puce. À chaque nuage de points conditionnel correspond un centre de gravité conditionnel matérialisé par la lettre G.
Des approches différentes selon les objectifs
On distingue généralement deux grandes approches :
- L’analyse discriminante peut être une technique descriptive. On parle dans ce cas d’analyse factorielle discriminante (ou analyse discriminante descriptive). L’objectif est de proposer un nouveau système de représentation, des variables latentes formées à partir de combinaisons linéaires des variables prédictives, qui permettent de discerner le plus possible les groupes d’individus. En ce sens, elle se rapproche de l’analyse factorielle car elle permet de proposer une représentation graphique dans un espace réduit, plus particulièrement de l’analyse en composantes principales calculée sur les centres de gravité conditionnels des nuages de points avec une métrique particulière. On parle également d’analyse canonique discriminante, notamment dans les logiciels anglo-saxons.
- L’analyse discriminante peut être prédictive. Il s’agit dans ce cas de construire une fonction de classement (règle d’affectation, …) qui permet de prédire le groupe d’appartenance d’un individu à partir des valeurs prises par les variables prédictives. En ce sens, cette technique se rapproche des techniques supervisées en apprentissage automatique telles que les arbres de décision, les réseaux de neurones, … Elle repose sur un cadre probabiliste. Le plus connu est certainement l’hypothèse de distribution multinormale (loi normale). Additionnée à l’hypothèse d’homoscédasticité, les nuages de points conditionnels ont la même forme, nous aboutissons à l’analyse discriminante linéaire. Elle est très séduisante dans la pratique car la fonction de classement s’exprime comme une combinaison linéaire des variables prédictives, facile à analyser et à interpréter. Cette technique est, avec la régression logistique, très utilisée dans le scoring, lorsque nous voulons par exemple caractériser l’appétence – la propension à acheter – d’un client face à un nouveau produit.
La distinction entre ces deux approches n’est pas aussi tranchée. Il est par exemple possible de dériver des règles géométriques d’affectation à partir de l’analyse factorielle discriminante.
Analyse discriminante descriptive
L’analyse discriminante descriptive (analyse factorielle discriminante, canonical discriminant analysis en anglais) est une technique de statistique exploratoire qui travaille sur un ensemble de
 observations décrites par
observations décrites par  variables, répartis en
variables, répartis en  groupes. Elle vise à produire un nouveau système de représentation, constitué de combinaisons linéaires des variables initiales, qui permet de séparer au mieux les
groupes. Elle vise à produire un nouveau système de représentation, constitué de combinaisons linéaires des variables initiales, qui permet de séparer au mieux les  catégories.
catégories.- L’analyse discriminante descriptive est une technique descriptive car elle propose une représentation graphique qui permet de visualiser les proximités entre les observations, appartenant au même groupe ou non.
- C’est aussi une technique explicative car nous avons la possibilité d’interpréter les axes factoriels, combinaisons linéaires des variables initiales, et ainsi comprendre les caractéristiques qui distinguent les différents groupes.
Contrairement à l’analyse discriminante prédictive, elle ne repose sur aucune hypothèse probabiliste. Il s’agit essentiellement d’une méthode géométrique.
Notations - Formulations
Données et notations
Nous disposons d’un échantillon de
 observations réparties dans
observations réparties dans  groupes d’effectifs
groupes d’effectifs  .
.Notons
 la variable définissant les groupes, elle prend ses valeurs dans
la variable définissant les groupes, elle prend ses valeurs dans  . Nous disposons de
. Nous disposons de  variables
variables  .
.Nous notons
 les centres de gravité des nuages de points conditionnels,
les centres de gravité des nuages de points conditionnels,  leurs matrice de variance-covariance.
leurs matrice de variance-covariance.Démarche
L’objectif de l’analyse discriminante est de produire un nouvel espace de représentation qui permet de distinguer le mieux les K groupes. La démarche consiste à produire une suite de variables discriminantes
 , non-corrélés deux à deux, tels que des individus du même groupe projetés sur ces axes soient le plus proches possibles les uns des autres, et que des individus de groupes différents soient le plus éloignés possibles.
, non-corrélés deux à deux, tels que des individus du même groupe projetés sur ces axes soient le plus proches possibles les uns des autres, et que des individus de groupes différents soient le plus éloignés possibles.- La dispersion à l’intérieur d’un groupe est décrite par la matrice de variance co-variance
 . Nous pouvons en déduire (à un facteur près) la dispersion intra-groupe
. Nous pouvons en déduire (à un facteur près) la dispersion intra-groupe 
- L’éloignement entre les groupes, entre les centres de gravité des groupes, est traduit par la matrice de variance co-variance inter-groupes (à un facteur près)
 , où
, où  est le centre de gravité du nuage de points global.
est le centre de gravité du nuage de points global.
- La dispersion totale du nuage est obtenue par la matrice de variance co-variance totale
 . En vertu du théorème d’Huyghens (qui est la généralisation mutlidimensionnelle de la formule de décomposition de la variance) :
. En vertu du théorème d’Huyghens (qui est la généralisation mutlidimensionnelle de la formule de décomposition de la variance) : 
Le premier axe factoriel sera donc défini par le vecteur directeur
 tel que l'on maximise la quantité
tel que l'on maximise la quantité  . La variance inter-classes sur ce premier axe factoriel
. La variance inter-classes sur ce premier axe factoriel  sera maximum.
sera maximum.Solution
La solution de ce problème d’optimisation linéaire passe par la résolution de l’équation
 . La réponse nous est directement fournie par le calcul des valeurs propres et vecteurs propres de la matrice
. La réponse nous est directement fournie par le calcul des valeurs propres et vecteurs propres de la matrice  .
.- Le premier axe factoriel
 est donc obtenu à l'aide du vecteur propre
est donc obtenu à l'aide du vecteur propre  correspondant à la plus grande valeur propre
correspondant à la plus grande valeur propre  . Le second axe factoriel est définie par le vecteur propre suivant, etc.
. Le second axe factoriel est définie par le vecteur propre suivant, etc.
- L'ensemble des axes factoriels est déterminée par les valeurs propres non-nulles de la matrice
 . Dans le cas usuel où
. Dans le cas usuel où  , nous obtenons
, nous obtenons  axes factoriels.
axes factoriels.
- Enfin, la variance inter-classes calculée sur l'axe factoriel
 , que l'on appelle également pouvoir discriminant de l'axe, est égale à la valeur propre
, que l'on appelle également pouvoir discriminant de l'axe, est égale à la valeur propre  associée.
associée.
Évaluation
L’évaluation se situe à deux niveaux : évaluer le pouvoir discriminant d’un axe factoriel ; évaluer le pouvoir discriminant d’un ensemble d’axes factoriels. L’idée sous-jacente est de pouvoir déterminer le nombre d’axes suffisants pour distinguer les groupes d’observations dans le nouveau système de représentation.
Bien entendu, ces évaluations n’ont de sens que si les groupes sont discernables dans l’espace de représentation initial. Il nous faut donc, dans un premier temps, apprécier dans quelle mesure les centres de gravité des groupes sont distincts. En d’autres termes, il s’agit de vérifier si la part de B dans l’équation V = B + W est assez importante pour que cela vaille la peine de la décomposer par la suite.
Test MANOVA
Le test global s’apparente à une analyse de variance multivariée à un facteur. Dans ce cadre, nous introduisons l’hypothèse que les observations suivent une loi normale multidimensionnelle. Nous retrouvons également ce test dans l’analyse discriminante prédictive (analyse discriminante linéaire). La statistique du test est le Lambda de Wilks qui est égal au rapport
 (| | désigne le déterminant de la matrice). En utilisant la transformation de Rao qui suit une loi de Fisher, nous pouvons déterminer si nous devons accepter ou réfuter l’hypothèse d’égalité des centres de gravité de groupes.
(| | désigne le déterminant de la matrice). En utilisant la transformation de Rao qui suit une loi de Fisher, nous pouvons déterminer si nous devons accepter ou réfuter l’hypothèse d’égalité des centres de gravité de groupes.Proportion de variance expliquée
Chaque axe rapporte une partie de la variance inter-classes B. Une approche simple pour apprécier l’importance d’un axe est de calculer la part de variance expliquée qu’elle porte, traduite par la valeur propre. La proportion de valeur propre, c.-à-d. le rapport entre la valeur propre de l’axe et la somme totale des valeurs propres de l’ensemble des axes, nous donne une bonne indication sur le rôle d’un axe.
Rapport de Corrélation
Une autre manière de rapporter l’importance d’un axe est de calculer le rapport de corrélation. Il s’appuie sur la formule de décomposition de la variance. Pour un axe factoriel
 , il est égal au ratio
, il est égal au ratio  (la somme des carrés inter-groupes divisé par la somme des carrés totale,
(la somme des carrés inter-groupes divisé par la somme des carrés totale,  représente une observation).
représente une observation).Un axe sera d’autant plus intéressant qu’il présente un rapport de corrélation élevé. Dans les logiciels anglo-saxons, la racine carrée du rapport de corrélation de l’axe
 est appelée la h-ème corrélation canonique.
est appelée la h-ème corrélation canonique.Test des racines successives
En introduisant de nouveau l’hypothèse de multinormalité et d’homoscédasticité (voir analyse discriminante prédictive), nous pouvons tester la nullité des
 derniers rapports de corrélation. Le test repose sur la statistique de Wilks
derniers rapports de corrélation. Le test repose sur la statistique de Wilks  . L’hypothèse nulle (nullité des
. L’hypothèse nulle (nullité des  rapports de corrélation) est infirmée pour les petites valeurs de
rapports de corrélation) est infirmée pour les petites valeurs de  .
.Tout comme pour le test global, une transformation est mise en œuvre pour retomber sur des lois de distribution d’usage courant. La transformation de Bartlett est souvent proposée dans les logiciels. Elle suit une loi du Khi-2 à
![[q \times (J-K+q+1)]\,](a/deaa162e362721eff802ace96375f885.png) degrés de liberté. L’hypothèse nulle est rejetée si la probabilité critique calculée est inférieure au risque de première espèce (niveau de confiance) que l’on s’est fixé.
degrés de liberté. L’hypothèse nulle est rejetée si la probabilité critique calculée est inférieure au risque de première espèce (niveau de confiance) que l’on s’est fixé.Nous retombons sur le test MANOVA global ci-dessus (Lambda de Wilks) si nous testons la nullité des rapports de corrélation sur tous les
 axes factoriels. En d'autres termes,
axes factoriels. En d'autres termes,  , ce qui est tout à fait naturel puisque cela revient à tester tous les axes.
, ce qui est tout à fait naturel puisque cela revient à tester tous les axes.Un exemple
Le fameux fichier IRIS permet d’illustrer la méthode. Il a été proposé et utilisé par Fisher lui-même pour illustrer l’analyse discriminante. Il comporte 150 fleurs décrites par 4 variables (longueur et largeur des pétales et sépales) et regroupées en 3 catégories (Setosa, Versicolor et Virginica).
L’objectif est de produire un plan factoriel (3 catégories ⇒ 2 axes) permettant de distinguer au mieux ces catégories, puis d’expliquer leurs positionnements respectifs.
Axes factoriels
Le calcul produit les résultats suivants.
Axe Val. propre Proportion Canonical R Wilks KHI-2 D.D.L. p-value 1 32.272 0.991 0.985 0.024 545.58 8 0.0 2 0.277 1.0 0.466 0.783 35.6 3 0.0 Les deux axes sont globalement significatifs. En effet, le lambda de Wilks de nullité des deux axes est égal à 0.023525 (
 ici). Le KHI-2 de Bartlett est égal à 545.57, avec un degré de liberté égal à (2 x (4-3+2+1)) = 8, il est très hautement significatif (p-value très petite).
ici). Le KHI-2 de Bartlett est égal à 545.57, avec un degré de liberté égal à (2 x (4-3+2+1)) = 8, il est très hautement significatif (p-value très petite).Nous constatons néanmoins que le premier axe traduit 99,1 % de la variance expliquée. Nous pouvons légitimement nous demander si le second axe est pertinent pour la discrimination des groupes. Il suffit pour cela de tester la nullité du dernier axe (
 ). Le lambda est plus élevé (0.78), ce qui se traduit par un KHI-2 plus faible (35.64) à (1 x (4-3+1+1)) = 3 degrés de liberté, il reste néanmoins significatif si l’on se fixe un niveau de confiance à 5 %.
). Le lambda est plus élevé (0.78), ce qui se traduit par un KHI-2 plus faible (35.64) à (1 x (4-3+1+1)) = 3 degrés de liberté, il reste néanmoins significatif si l’on se fixe un niveau de confiance à 5 %.Partant de ce résultat, nous serions amenés à conserver les deux axes. Nous verrons plus bas que ce résultat est à relativiser.
Représentation graphique
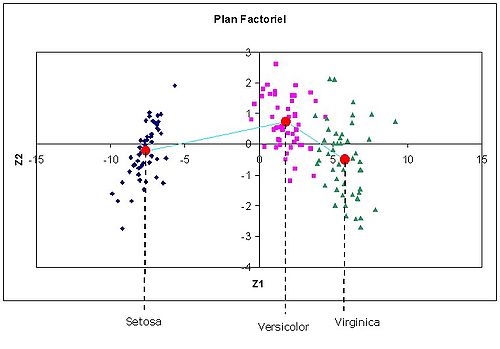
En projetant les points dans le plan factoriel, nous obtenons le positionnement suivant.
Nous distinguons bien les trois catégories de fleurs. Nous constatons également que le premier axe permet déjà de les isoler convenablement. Sur le second axe, même si les centres de gravité des groupes semblent distincts, la différenciation n’est pas aussi tranchée.
Nous retrouvons bien dans ce graphique ce que l’on pressentait avec la proportion de variance expliquée. Le premier axe suffit largement pour discriminer les groupes. Le second axe, même s’il est statistiquement significatif, n’apporte pas un réel complément d’informations.
Très souvent, les techniques visuelles emmènent un contrepoint très pertinent aux résultats numériques bruts.
Projection des individus supplémentaires
Pour projeter des observations supplémentaires dans le plan factoriel, les logiciels fournissent les équations des fonctions discriminantes. Il suffit de les appliquer sur la description de l’individu à classer pour obtenir ses coordonnées dans le nouveau repère.
Dans l’exemple IRIS, nous obtenons les coefficients suivants.
Variables Axe 1 Axe 2 Sepal Length -0.819 -0.033 Sepal Width -1.548 -2.155 Petal Length 2.185 0.930 Petal Width 2.854 -2.806 Constante -2.119 6.640 Interprétation des axes
Dernier point, et non des moindres, il nous faut comprendre le positionnement relatif des groupes, c.-à-d. expliquer à l’aide de variables initiales l’appartenance aux catégories.
Pour cela, à l’instar des techniques factorielles telles que l’analyse en composantes principales (ACP) -- l’analyse factorielle discriminante peut être vue comme un cas particulier de l’ACP d’ailleurs -- les logiciels fournissent la matrice de corrélation. À la différence de l’ACP, trois types de corrélations peuvent être produits : la corrélation globale entre les axes et les variables initiales ; la corrélation intra-classes, calculée à l’intérieur des groupes ; la corrélation inter-classes calculée à partir des centres de gravité des groupes pondérés par leurs fréquences.
Dans l’exemple IRIS, si nous nous en tenons au premier axe, nous obtenons les corrélations suivantes.
Variables Total Intra-groupes Inter-groupes Sep Length 0.792 0.222 0.992 Sep Width -0.523 -0.116 -0.822 Pet Length 0.985 0.705 1.000 Pet Width 0.973 0.632 0.994 La corrélation inter-classes qui traduit le positionnement des groupes sur les axes indique ici que les Virginica ont plutôt des longueurs de sépales, des longueurs et des largeurs de pétales importantes. Les Setosa possèdent à l’inverse des longueurs de sépales, des longueurs et des largeurs de pétales réduites. Les Versicolor occupent une position intermédiaire.
La lecture est inversée concernant la largeur des sépales.
Références
- M. Bardos, Analyse Discriminante - Application au risque et scoring financier, Dunod, 2001.
- (fr) Gilbert Saporta, Probabilités, Analyse des données et Statistique, 2006 [détail des éditions]
- L. Lebart, A. Morineau, M. Piron, Statistique Exploratoire Multidimensionnelle, Dunod, 2000.
- M. Tenenhaus, Méthodes Statistiques en Gestion, Dunod, 1996.
- Michel Volle, Analyse des données, Economica, 4e édition, 1997, ISBN 2-7178-3212-2
- Portail des probabilités et des statistiques
Wikimedia Foundation. 2010.