Marching Cubes

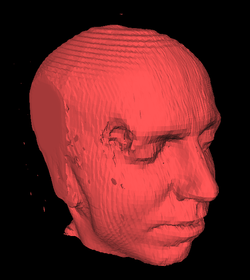Tête et structures cérébrales (cachées) obtenues par l'application des marching-cubes sur 150 tranches provenant d'un IRM (env. 150'000 triangles)

Les « marching cubes » désignent un algorithme d'infographie publié à la conférence SIGGRAPH 1987 par Lorensen et Cline. Ils permettent de générer un objet polygonal à partir d'un champ scalaire en trois dimensions (son unité élémentaire est souvent appelée voxel), en principe généré par approximation d'une isosurface.

Il est le pendant 3D de l'algorithme des « marching squares ».

Principe de fonctionnement

Cet algorithme parcourt le champ scalaire, prenant huit points à la fois (définissant ainsi un cube imaginaire), et détermine les polygones à créer (si polygone à créer il y a) pour représenter une partie de l'isosurface contenue dans ce cube.

Ceci fonctionne en créant un index dans un tableau précalculé des 256 configurations de polygones possibles (2⁸ = 256) dans un cube, en traitant chacune des 8 valeurs scalaires comme un bit dans un nombre entier de 8 bits. Si la valeur scalaire est supérieure à la valeur de l'isosurface (i.e., est à l'intérieur de la surface), alors le bit correspondant est mis à 1, sinon il est mis à 0. La valeur finale après le test des 8 points est l'index de la bonne configuration polygonale dans le tableau précalculé.

Finalement, chaque sommet des polygones générés est placé à sa position finale le long de l'arête du cube, en interpolant linéairement les deux valeurs scalaires connectés par cette arête.

Les 256 valeurs du tableau de configuration des polygones sont précalculées par réflexion et symétrie à partir de 15 cas possibles.

Les 15 cas possibles de configuration des polygones

La valeur à chaque point du champ scalaire est aussi utilisée pour calculer le vecteur normal de l'isosurface passant en ce point. Ce calcul est basé sur le gradient du champ. Il est donc possible d'interpoler ces valeurs le long de chaque arête de chaque cube de façon à obtenir la normale des points sur la surface. L'interpolation permet d'éviter un calcul analytique du gradient pour une position quelconque. Le calcul des normales permet l'ombrage de l'objet par la suite.

Applications

Les applications principales de cet algorithme sont du domaine de la visualisation médicale, comme la reconstruction de surfaces à partir des images issues de scanners ou d'IRM. L'algorithme peut également être mis en œuvre pour des effets spéciaux et des outils infographiques comme la modélisation 3D d'objets organiques (metaballs et toutes autres isosurfaces).

Brevets

Cet algorithme est le premier exemple de brevet logiciel dans le domaine de l'infographie. Un algorithme similaire, appelé « Marching Tetrahedrons », a été développé de façon à contourner ce brevet et quelques problèmes topologiques mineurs liés à l'utilisation de cubes. Le brevet couvrant les Marching cubes a expiré : il a été déposé le 5 juin 1985 au Bureau des brevets des États-Unis, le délai de 20 ans ayant expiré, son implémentation et son utilisation sont désormais libres de droit.

Le problème du brevet ne se posait pas pour les utilisations à l'intérieur d'un pays ne couvrant pas les brevets logiciels, comme la France, ou la majorité des pays d'Europe^[1].

Voir aussi

• marching tetrahedra

Références

• Brevet original décrivant l'algorithme

Liens externes

• "The Marching Cubes Algorithm", voir crédits sur la page

• Portail de l’informatique