- Isopleure
-
Polygone équilatéral
En géométrie, un polygone équilatéral est un polygone qui a tous ses côtés de même longueur.
Un polygone équilatéral qui est convexe et inscrit dans un cercle est un polygone régulier.
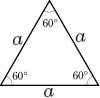
Un triangle équilatéral est un triangle dont les longueurs des côtés sont égales. Tous les triangles équilatéraux sont similaires avec des triangles ayant des angles de 60 degrés.
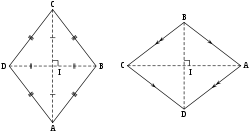
Tout quadrilatère équilatéral est un losange.
Tout polygone à n-côtés qui a n côtés de longueurs égales peut être considéré comme équilatéral. Un polygone équilatéral n'est pas nécessairement convexe : par exemple considérer le pentagone étoilé obtenu en joignant, de deux en deux, les sommets d'un pentagone régulier.
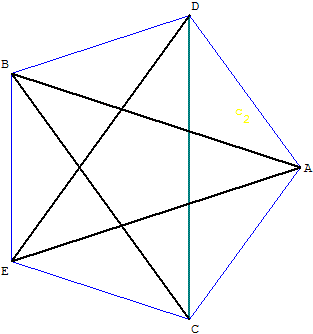
Le pentagone croisé ABCDE est obtenu à partir du pentagone convexe ADBEC.
Anecdote
Du grec isos qui signifie égal, et pleura côtés, isopleure était le mot anciennement utilisé.
Liens externes
- Triangle équilatéral avec une animation interactive.
- Portail de la géométrie
Catégorie : Polygone
Wikimedia Foundation. 2010.