Loi De Peirce

La loi de Peirce est la proposition 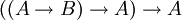où désigne l'implication. Elle a été proposée par le logicien et philosophe Charles Sanders Peirce.

Cette formule, valide en logique classique, est invalide en logique intuitionniste. Cela signifie que, bien que ne possédant pas de référence explicite à la négation, la loi de Peirce est directement liée à la façon dont on traite celle-ci. Ainsi, on peut montrer que, en logique intuitionniste, il y a équivalence entre loi de Peirce, règle d'élimination de la double négation ou principe du tiers exclu. L'ajout d'un seul de ces principes à la logique intuitionniste redonne la totalité de la logique classique.

Démonstration de la loi de Peirce en logique classique

L'un des principes de la logique classique est le raisonnement par l'absurde. Pour montrer une proposition A, on suppose que A est faux. Si on aboutit à une contradiction, alors on peut en déduire la validité de A.

Pour montrer que l'implication 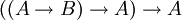est valide, nous allons donc supposer 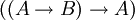et nous devons montrer que A est vraie. Raisonnons par l'absurde et supposons que A est fausse. Mais si A est fausse, alors l'implication 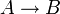est vraie. Comme on a supposé 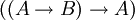et que l'hypothèse 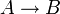est vraie, la conclusion A est également vraie, d'où une contradiction.

Logique intuitionniste et loi de Peirce

La logique intuitionniste traite la négation de la façon suivante (on suppose le lecteur familier avec des notations qui sont précisées par exemple dans l'article calcul des propositions) :

• Si on a à la fois une proposition A et sa négation 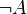, alors on a une contradiction, notée 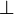(règle dite d'élimination de la négation).
• Si une proposition A conduit à une contradiction, alors c'est que 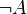est valide (règle dite d'introduction de la négation). Dans ce sens, 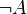n'est rien d'autre qu'un synonyme de .
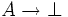• Si un raisonnement conclut à une contradiction, alors on peut en déduire la validité de toute proposition (règle dite de l'absurdité intuitionniste). Cette règle est remplacée, en logique classique, par le raisonnement par l'absurde.

Considérons alors les formules suivantes :

• Elimination de la double négation :
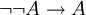
• Tiers exclu :
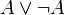
• Contraposition :

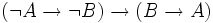
Plaçons nous dans le cadre de la logique intuitionniste et ajoutant à cette logique la loi de Peirce. Nous allons montrer que les trois formules précédentes sont valides et qu'on obtient la logique classique. Remarquons d'abord que, si on applique la loi de Peirce en remplaçant B par une proposition contradictoire, on obtient la variante suivante .

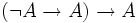Preuve de l'élimination de la double négation : Soit comme hypothèse une proposition de la forme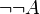 . Si on suppose de plus 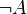, on obtient une contradiction (une proposition et sa négation) d'où l'on peut déduire A par la règle de l'absurdité intuitionniste. On a donc montré l'implication 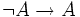. Appliquant la variante ci-dessus de la loi de Peirce, on en déduit la validité de A. On a donc montré que .

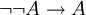L'élimination de la double négation est à la base du raisonnement par l'absurde. En effet, si 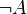conduit à une contradiction, alors on a 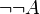par la règle d'introduction de la négation, et donc on a A par élimination de la double négation. On a donc montré que l'adjonction de la loi de Peirce à la logique intuitionniste redonne bien la logique classique.

Preuve du tiers exclu : c'est en fait une conséquence directe de l'élimination de la double négation ou du raisonnement par l'absurde. Si on a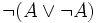 alors on a 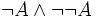, ce qui est contradictoire. Donc on a 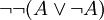et donc 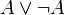par élimination de la double négation.

Preuve de la contraposition : c'est également une conséquence de l'élimination de la double négation. Soit la proposition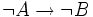 . Montrons que 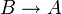. Pour cela supposons B et montrons A. Si on avait 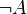, on aurait 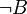, ce qui est contradictoire avec l'hypothèse. On a donc 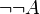, et par élimination de la double négation, on a A.

Voir aussi

• logique classique
• logique intuitionniste
• logique minimale

• Portail des mathématiques
• Portail de la philosophie
• Portail de la logique