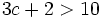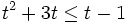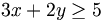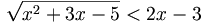Inéquation (mathématiques élémentaires)

Cet article fait partie de la série Mathématiques élémentaires

Algèbre

Logique

Arithmétique

Probabilités

Statistiques

Une inéquation est une question, sous forme d'une inégalité entre deux quantités algébriques. Cette inégalité contient des inconnues. Résoudre une inéquation, c'est trouver les valeurs de ces inconnues qui rendent vraie l'inégalité.

Il faut évidemment que le symbole < ou ≤ ait un sens. Il est donc nécessaire, en mathématiques élémentaires, que les inconnues appartiennent à l'ensemble des réels R ou à une partie de R. En particulier, il est impossible de travailler dans l'ensemble des complexes C.

Exemples:

Règles opératoires

La résolution des inéquations va demander la connaissance de quelques règles opératoires s'apparentant à celles déjà évoquées pour la résolution des équations mais avec de subtiles et fondamentales différences :

1. Transitivité de l'inégalité

si a < b et b < c alors a < c (propriétés valables pour deux inégalités de même nature : deux inégalités « < », ou deux inégalités « > » ou deux inégalités « ≤ » ou deux inégalités « ≥ »

2. On peut ajouter un même nombre aux deux membres d'une inégalité sans en changer la nature.

si a < b alors a + c < b + c

3. On peut soustraire un même nombre aux deux membres d'une inégalité sans en changer la nature.

si a < b alors a - c < b - c

4. On peut multiplier par un même nombre strictement positif les deux membres d'une inégalité sans en changer la nature.

si a < b et si c > 0 alors ac < bc

si on multiplie par un nombre négatif, l'inégalité change de sens

si a < b et si c < 0 alors ac > bc

5. On peut diviser par un même nombre strictement positif les deux membres d'une inégalité sans en changer la nature.

si a < b et si c > 0 alors a/c < b/c

si on divise par une nombre négatif, l'inégalité change de sens

si a < b et si c < 0 alors a/c > b/c

À ces quelques règles, on ajoutera les quatre règles suivantes :

• l'inégalité est compatible avec l'addition, c'est-à-dire que l'on peut additionner membre à membre deux inégalités de même nature

si a < b et a' < b' alors a + a' < b + b'

mais on ne peut pas soustraire membre à membre deux inégalités de même sens (car une soustraction est une addition de l'opposé et la prise de l'opposé change le sens de l'inégalité).

• l'inégalité est compatible avec la multiplication seulement pour des nombres positifs, c'est-à-dire que l'on peut multiplier membre à membre deux inégalités constituées de nombres positifs entre deux inégalités de même sens

si 0 < a < b et 0 < a' < b' alors aa' < bb'

• La prise de l'opposé ou celle de l'inverse (pour des nombres de même signe) est une fonction décroissante, c'est-à-dire qu'elle change le sens de l'inégalité.

si a < b alors -a > -b

si 0 < a < b alors 1/a > 1/b

si a < b < 0 alors 1/a > 1/b

• la règle des signes : le produit de deux quantités de même signe est positif, le produit de deux quantités de signes opposés est négatif.

Résolution d'inéquations particulières

• Inéquation du premier degré
• Inéquation du second degré
• Inéquation se résolvant par tableau de signes
• Inéquation linéaires à plusieurs inconnues
• Inéquation avec racine carrée
• Tracer une inéquation/inégalité sur un graphique

Voir aussi

• Relation d'ordre
• Algèbre (mathématiques élémentaires)

• Portail des mathématiques