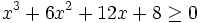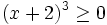- Inequation se resolvant par tableau de signes
-
Inéquation se résolvant par tableau de signes
Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques Cas d'un produit
Exemple 1 : soit l'inéquation
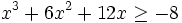.Pour résoudre ce type d'inéquations par tableau de signes, on regroupe tout dans le premier membre pour avoir zéro dans le second puis on factorise le premier membre obtenu.
Ceci grâce à la règle :
- Pour connaître le signe d'un produit, il suffit de chercher celui de chacun de ses facteurs, puis d'en déduire celui du produit grâce à la règle des signes.
Ici, on a
puis
d'après l'identité remarquable
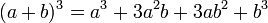.Résoudre cette inéquation revient à chercher le signe de
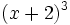, c'est-à-dire celui de 
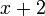.On a alors le tableau de signes suivant :
valeurs de 
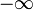
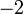
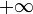
signe de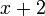 
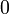
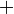
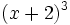
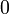
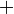
signe de On en conclut que l'ensemble des solutions de cette inéquation est:
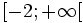.Cas d'un quotient
Exemple 2: Soit l'inéquation
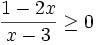.La règle vue plus haut pour un produit est valable aussi pour un quotient, à condition d'avoir vérifié pour quelle(s) valeur(s) ce quotient n'existe pas. Ici, il ne faut pas que
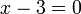donc il ne faut pas que 
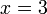.Alors on fait le tableau de signes suivant:
valeurs de 
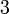
signe de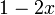 
+ 0 − | − signe de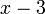 
− | − 0 + signe de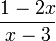 
− 0 + | | − L'ensemble des solutions est donc :
.
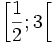Portail des mathématiques
Catégorie : Mathématiques élémentaires
Wikimedia Foundation. 2010.
