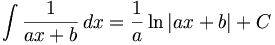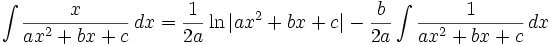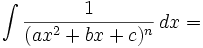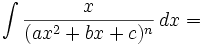Intégration de fonctions rationnelles
Contenu soumis à la licence CC-BY-SA. Source : Article Intégration de fonctions rationnelles de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
FONCTIONS (REPRÉSENTATION ET APPROXIMATION DES) — Il arrive très souvent que, dans les problèmes issus des mathématiques ou des autres sciences, les fonctions qui interviennent soient définies par des procédés qui ne permettent pas d’étudier de manière efficace leurs propriétés. C’est le cas des … Encyclopédie Universelle
FONCTIONS ANALYTIQUES - Fonctions d’une variable complexe — On se propose, dans ce premier article, d’exposer, avec des démonstrations quasiment complètes, les résultats les plus élémentaires de la théorie des fonctions analytiques d’une variable complexe; les deux derniers chapitres sont consacrés à… … Encyclopédie Universelle
Primitives de fonctions circulaires réciproques — Cet article donne les primitives des fonctions réciproques des fonctions circulaires. Elles s obtiennent dans la plupart des cas par intégration par parties … Wikipédia en Français
Primitives de fonctions hyperboliques réciproques — Cet article donne les primitives des fonctions réciproques des fonctions hyperboliques. Elles s obtiennent dans la plupart des cas par intégration par parties … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Table de primitives — Le calcul d une primitive d une fonction est l une des deux opérations de base de l analyse et comme cette opération est délicate à effectuer, à l inverse de la dérivation, des tables de primitives connues sont souvent utiles. Nous savons qu une… … Wikipédia en Français
Algorithme de Risch — L’algorithme de Risch, dû à Robert Risch (de), est un algorithme destiné aux systèmes de calcul formel, permettant de calculer des primitives, c est à dire de déterminer une fonction, connaissant sa dérivée. L’algorithme transforme ce… … Wikipédia en Français
Остроградский, Михаил Васильевич — профессор математики, ординарный академик Императорской Академии Наук. М. В. Остроградский родился 12 сентября 1801 года в принадлежавшей его отцу деревне Пашенной, Кобелякского уезда, Полтавской губернии, где и провел свои детские годы.… … Большая биографическая энциклопедия
EXPONENTIELLE ET LOGARITHME — Pour les constructeurs des premières tables, les logarithmes étaient avant tout un outil de calcul numérique; mais leur importance n’a cessé de croître. Il suffira de feuilleter cette encyclopédie pour constater que, de nos jours, les logarithmes … Encyclopédie Universelle
SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES — Sans doute née avec le mémoire que Poincaré écrivit en 1881 «sur les courbes définies par des équations différentielles», où l’étude quantitative (analytique) locale des équations différentielles dans le champ complexe est remplacée par leur… … Encyclopédie Universelle
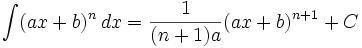 (n ∈ ℤ\{-1})
(n ∈ ℤ\{-1})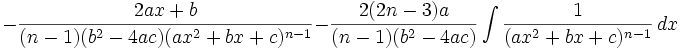
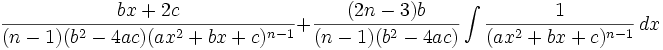 Catégories : Primitive | Analyse réelle
Catégories : Primitive | Analyse réelle