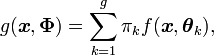Modele de melanges gaussiens

Modele de melanges gaussiens

Modèle de mélanges gaussiens

Dans les modèles de mélanges, fréquemment utilisées en classification automatique, on considère qu'un échantillon de données suit, non pas une loi de probabilité usuelle, mais une loi dont la fonction de densité est une densité mélange.

Bien que n'importe quelle loi puisse être utilisée, la plus courante est la loi normale dont la fonction de densité est une gaussienne. On parle alors de mélange gaussien.

Sommaire

Utilisation en classification automatique

Le problème classique de la classification automatique est de considérer qu'un échantillon de données provienne d'un nombre de groupes inconnus a priori qu'il faut retrouver. Lorsqu'on part du postulat que ces groupes suivent une loi de probabilité (quelconque), alors on se place nécessairement dans le cadre des modèles de mélanges. Si en plus, on considère que les lois que suivent les individus sont normales, alors on se place dans le cadre des modèles de mélanges gaussiens.

Par la suite, on notera 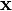\mathbf{x}\, un échantillon composé de n individus 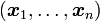\left(\boldsymbol{x}_1,\dots,\boldsymbol{x}_n\right) appartenant à 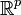\mathbb{R}^p (i.e. caractérisés par p variables continues). Dans le cadre des modèles de mélanges, on considère que ces individus appartiennent chacun à un des g (g étant fixé a priori) 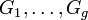G_1,\dots,G_g suivant chacun une loi normale de moyenne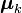 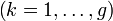\boldsymbol{\mu}_k\, \left(k=1,\dots,g\right) et de matrice de variance-covariance 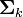\boldsymbol{\Sigma}_k\,. D'autre part, en notant 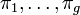\pi_1,\dots,\pi_g les proportions des différents groupes, 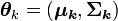\boldsymbol{\theta}_k=\left(\boldsymbol{\mu_k},\boldsymbol{\Sigma_k}\right) le paramètre de chaque loi normale et 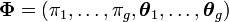\boldsymbol{\Phi}=\left(\pi_1,\dots,\pi_g,\boldsymbol{\theta}_1,\dots,\boldsymbol{\theta}_g\right) le paramètre global du mélange, la loi mélange que suit l'échantillon peut s'écrire

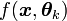g(\boldsymbol{x},\boldsymbol{\Phi})=\sum_{k=1}^g\pi_kf(\boldsymbol{x},\boldsymbol{\theta}_k),

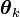avec f(\boldsymbol{x},\boldsymbol{\theta}_k)\, la loi normale multidimensionnelle paramétrée par \boldsymbol{\theta}_k\,.

La principale difficulté de cette approche consiste à déterminer le meilleur paramètre 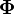\boldsymbol{\Phi}. Pour cela, on cherche habituellement le paramètre qui maximise la vraisemblance, donnée dans ce cas, par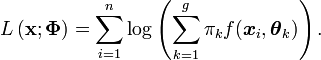

L\left(\mathbf{x};\boldsymbol{\Phi}\right)=\sum_{i=1}^n\log\left(\sum_{k=1}^g\pi_kf(\boldsymbol{x}_i,\boldsymbol{\theta}_k)\right).

Bien que ce problème puisse sembler particulièrement hardu, l'algorithme EM permet de lever cette difficulté.

Une fois l'estimation effectuée, il s'agit d'attribuer à chaque individu la classe à laquelle il appartient le plus probablement. Pour cela, on utilise la règle d'inversion de Bayes. D'après celle-ci, on a

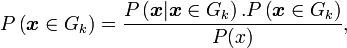
P\left(\boldsymbol{x}\in G_k\right)=\frac{P\left(\boldsymbol{x}|\boldsymbol{x}\in G_k\right).P\left(\boldsymbol{x}\in G_k\right)}{P(x)},

ce qui se traduit, dans notre cas, par

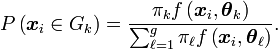
P\left(\boldsymbol{x}_i\in G_k\right)=\frac{\pi_kf\left(\boldsymbol{x}_i,\boldsymbol{\theta}_k\right)}{\sum_{\ell=1}^g\pi_\ell f\left(\boldsymbol{x}_i,\boldsymbol{\theta}_\ell\right)}.

Il suffit alors d'attribuer chaque individu 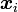\boldsymbol{x}_i à la classe pour laquelle la probabilité a posteriori 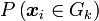P\left(\boldsymbol{x}_i\in G_k\right) est la plus grande.

Modèles parcimonieux

Un problème qu'on peut rencontrer lors de la mise en œuvre des modèles de mélange concerne la taille du vecteur de paramètres à estimer. Dans le cas d'un mélange gaussien de g composantes de dimension p le paramètre est de dimension k(1 + p + p2) − 1. La quantité de données nécessaire à une estimation fiable peut alors être trop importante par rapport au coût de leur recueil.

Une solution couramment employée est de déterminer quelles sont, parmi toutes les variables disponibles, celles qui apporteront le plus d'information à l'analyse et d'éliminer les variables ne présentant que peu d'intérêt. Cette technique, très employée dans des problèmes de discrimination l'est moins dans les problèmes de classification.

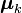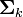Une méthode alternative consiste à considérer des modèles dits parcimonieux dans lesquels on contraint le modèle initial de manière à n'estimer qu'un nombre plus restreint de paramètres. Dans le cas gaussien, la paramétrisation synthétique des lois de probabilités grâce à deux ensembles \boldsymbol{\mu}_k et \boldsymbol{\Sigma}_k de paramètres permet des ajouts de contraintes relativement simples. Le plus souvent, ces contraintes ont une signification géométrique en termes de volumes, d'orientation et de forme.

En notant Bk la matrice des valeurs propres de 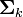\boldsymbol{\Sigma}_k et Dk la matrice de ses vecteurs propres, on peut noter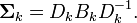

\boldsymbol{\Sigma}_k=D_kB_kD_k^{-1}.

D'autre part, Bk peut également être décomposée en Bk = λkAk où λk est un réel et Ak une matrice dont le déterminant vaut 1. En utilisant ces notations, on peut considérer que λk représente le volume de la classe, la matrice Ak représente sa forme et Dk son orientation.

Il est alors possible d'ajouter des hypothèses sur formes, des volumes ou les orientations des classes :

  • Formes quelconques : En fixant des contraintes d'égalité entre les Ak, les Dk ou les λk, on peut générer 8 modèles différents. On peut par exemple considérer des volumes et des formes identiques mais orientées différemment, ou encore des formes et orientations identiques avec des volumes différents, etc.
  • Formes diagonales : En considérant que les matrices Dk sont diagonales, on oblige les classes à être alignées sur les axes. Il s'agit en fait de l'hypothèse d'indépendance conditionnelle dans laquelle les variables sont indépendantes entre elles à l'intérieur d'une même classe.
  • Formes sphériques : En fixant Ak = I, on se place dans le cas ou les classes sont de formes sphériques, c’est-à-dire que les variances de toutes les variables sont égales à l'intérieur d'une même classe.

Liens externes

Voir aussi

  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
  • Portail de l’informatique Portail de l’informatique
Ce document provient de « Mod%C3%A8le de m%C3%A9langes gaussiens ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Modele de melanges gaussiens de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Modèle De Mélanges Gaussiens — Dans les modèles de mélanges, fréquemment utilisées en classification automatique, on considère qu un échantillon de données suit, non pas une loi de probabilité usuelle, mais une loi dont la fonction de densité est une densité mélange. Bien que… …   Wikipédia en Français

  • Modèle de mélanges gaussiens — Un modèle de mélange gaussien (usuellement abrégé par l acronyme anglais GMM pour Gaussian Mixture Model) est un modèle statistique exprimé selon une densité mélange. Elle sert usuellement à estimer paramétriquement la distribution de variables… …   Wikipédia en Français

  • Modèle de mixture gaussienne — Modèle de mélanges gaussiens Dans les modèles de mélanges, fréquemment utilisées en classification automatique, on considère qu un échantillon de données suit, non pas une loi de probabilité usuelle, mais une loi dont la fonction de densité est… …   Wikipédia en Français

  • Machine a vecteurs de support — Machine à vecteurs de support Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de… …   Wikipédia en Français

  • Machine À Vecteurs De Support — Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de discrimination[1] et de régression. Les SVM… …   Wikipédia en Français

  • Machine à vecteur de support — Machine à vecteurs de support Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de… …   Wikipédia en Français

  • Machine à vecteurs de support — Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de discrimination[note 1] et de régression. Les… …   Wikipédia en Français

  • Separateur a Vaste Marge — Machine à vecteurs de support Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de… …   Wikipédia en Français

  • Support vector machine — Machine à vecteurs de support Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de… …   Wikipédia en Français

  • Séparateur à Vaste Marge — Machine à vecteurs de support Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d apprentissage supervisé destinées à résoudre des problèmes de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”