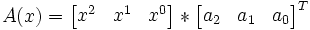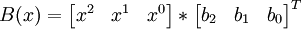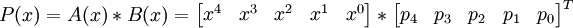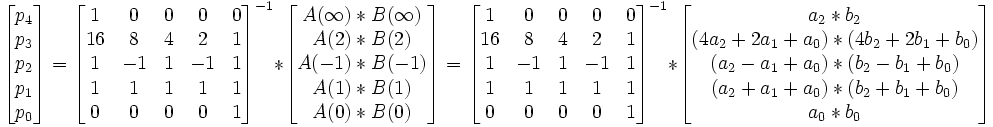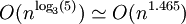Algorithme de Toom-Cook

Algorithme de Toom-Cook

Algorithme Toom-Cook

Toom-Cook, aussi appelé Toom-3, est une technique de multiplication utilisée pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on effectuera les calculs.

Multiplier deux nombres revient à multiplier deux polynômes

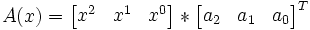
A(x) = \begin{bmatrix} x^2 & x^1 & x^0 \end{bmatrix} * \begin{bmatrix} a_2 & a_1 & a_0 \end{bmatrix}^T

et

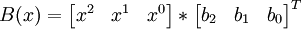
B(x) = \begin{bmatrix} x^2 & x^1 & x^0 \end{bmatrix} * \begin{bmatrix} b_2 & b_1 & b_0 \end{bmatrix}^T

ce qui donne un troisième polynôme

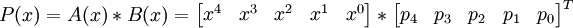
P(x) = A(x)*B(x) = \begin{bmatrix} x^4 & x^3 & x^2 & x^1 & x^0 \end{bmatrix} * \begin{bmatrix} p_4 & p_3 & p_2 & p_1 & p_0 \end{bmatrix}^T

En l'évaluant en cinq points

\begin{bmatrix} P(\infty) \\ P( 2) \\ P(-1) \\ P( 1) \\ P( 0) \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} p_4 \\ p_3 \\ p_2 \\ p_1 \\ p_0 \end{bmatrix}

ses coefficients peuvent être déterminés

\begin{bmatrix} p_4 \\ p_3 \\ p_2 \\ p_1 \\ p_0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{-1} * \begin{bmatrix} P(\infty) \\ P( 2) \\ P(-1) \\ P( 1) \\ P( 0) \end{bmatrix}

Ce calcul nécessite cinq multiplications trois fois plus simples et quelques additions

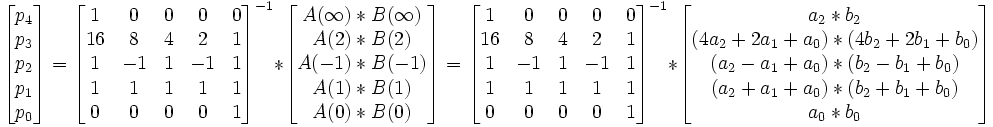
\begin{bmatrix} p_4 \\ p_3 \\ p_2 \\ p_1 \\ p_0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{-1} * \begin{bmatrix} A(\infty)*B(\infty) \\ A( 2)*B( 2) \\ A(-1)*B(-1) \\ A( 1)*B( 1) \\ A( 0)*B( 0) \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{-1} * \begin{bmatrix} a_2*b_2 \\ (4a_2+2a_1+a_0)*(4b_2+2b_1+b_0) \\ (a_2-a_1+a_0)*(b_2-b_1+b_0) \\ (a_2+a_1+a_0)*(b_2+b_1+b_0) \\ a_0*b_0 \end{bmatrix}

La complexité est donc

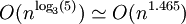
O(n^{\log _3 (5)}) \simeq O(n^{1.465})

Voir aussi

Références

  • Тоом Андрей Леонович, О сложности схемы из функциональных элементов, реализующей умножение целых чисел, Доклады Академии Наук СССР, T.150, N°3, pagg.496-498 [1]
  • D. Knuth. The Art of Computer Programming, Volume 2. Troisième édition, Addison-Wesley, 1997.
  • R. Crandall & C. Pomerance. Prime Numbers - A Computational Perspective. Seconde édition, Springer, 2005.
  • Toom 3-Way Multiplication, documentation de GMP
Algorithmes de multiplication
Produit de matrices Naïf  · Strassen  · Coppersmith-Winograd
Produit d'entiers Naïf  · Karatsuba  · Toom-Cook  · Schönhage-Strassen  · Fürer
Ce document provient de « Algorithme Toom-Cook ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algorithme de Toom-Cook de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Algorithme Toom-Cook — L algorithme de Toom Cook, aussi appelé Toom 3, est un algorithme de multiplication dû à Andrei Toom (en) et Stephen Cook, utilisé pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on… …   Wikipédia en Français

  • Toom-Cook — Algorithme Toom Cook Toom Cook, aussi appelé Toom 3, est une technique de multiplication utilisée pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on effectuera les calculs. Multiplier deux …   Wikipédia en Français

  • Algorithme de Karatsuba — L algorithme de Karatsuba (1960) est une méthode permettant de multiplier rapidement deux nombres avec une complexité en au lieu de O(n2) pour la méthode naïve. Note : . Énoncé Pour multiplier deux nombres de n chiffres, la méthode naïve… …   Wikipédia en Français

  • Algorithme De Karatsuba — L algorithme de Karatsuba (1960) est une méthode permettant de multiplier rapidement deux nombres avec une complexité en au lieu de O(n2) pour la méthode naïve. Note : . Sommaire 1 Énoncé …   Wikipédia en Français

  • Algorithme de karatsuba — L algorithme de Karatsuba (1960) est une méthode permettant de multiplier rapidement deux nombres avec une complexité en au lieu de O(n2) pour la méthode naïve. Note : . Sommaire 1 Énoncé …   Wikipédia en Français

  • Algorithme De Multiplication — Les techniques de multiplication permettent de calculer le résultat d une multiplication. Graphiquement, il s agit de transformer un rectangle multiplicateur × multiplicande en une ligne, en conservant le nombre d éléments. Exemples: Sommaire 1… …   Wikipédia en Français

  • Algorithme De Strassen — L’algorithme de Strassen est un algorithme calculant le produit de deux matrices carrées de taille n. Il est dû à Volker Strassen en 1969.[1] La complexité de l algorithme est en O(n2,807), soit une meilleure complexité que la multiplication… …   Wikipédia en Français

  • Algorithme de strassen — L’algorithme de Strassen est un algorithme calculant le produit de deux matrices carrées de taille n. Il est dû à Volker Strassen en 1969.[1] La complexité de l algorithme est en O(n2,807), soit une meilleure complexité que la multiplication… …   Wikipédia en Français

  • Algorithme De Coppersmith-Winograd — L’algorithme de Coppersmith Winograd est un algorithme de calcul du produit de deux matrices carrées de taille n du à Don Coppersmith et Shmuel Winograd en 1987[1]. Sa complexité algorithmique est en ce qui en fait l algorithme le plus efficace… …   Wikipédia en Français

  • Algorithme de Coppersmith–Winograd — Algorithme de Coppersmith Winograd L’algorithme de Coppersmith Winograd est un algorithme de calcul du produit de deux matrices carrées de taille n du à Don Coppersmith et Shmuel Winograd en 1987[1]. Sa complexité algorithmique est en ce qui en… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”