Algorithme de Coppersmith–Winograd
- Algorithme de Coppersmith–Winograd
-
Algorithme de Coppersmith-Winograd
L’algorithme de Coppersmith-Winograd est un algorithme de calcul du produit de deux matrices carrées de taille n du à Don Coppersmith et Shmuel Winograd en 1987[1]. Sa complexité algorithmique est en 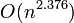 ce qui en fait l'algorithme le plus efficace en théorie. Rien n'indique que la complexité est optimale, l'exposant 2 étant généralement considéré comme optimal[2].
ce qui en fait l'algorithme le plus efficace en théorie. Rien n'indique que la complexité est optimale, l'exposant 2 étant généralement considéré comme optimal[2].
L'algorithme est utilisé comme brique de base pour prouver des résultats théoriques sur la complexité algorithmique. Mais aucune implémentation de l'algorithme n'est utilisée car la constante dans le grand O est prohibitive.
L'algorithme de Coppersmith-Winograd a été retrouvé par des méthodes de représentation des groupes finis[3].
Voir aussi
Références
- ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, pages 1–6, 1987.
- ↑ On sait que l'exposant ne peut être inférieur à 2 puisque l'algorithme doit au moins lire les n2 entrées de la matrice.
- ↑ Henry Cohn, Robert Kleinberg, Balazs Szegedy, and Chris Umans. Group-theoretic Algorithms for Matrix Multiplication. Proceedings of the 46th Annual Symposium on Foundations of Computer Science, 23-25 October 2005, Pittsburgh, PA, IEEE Computer Society, pp. 379–388. Disponible sur arXiv ici.
 Portail des mathématiques
Portail des mathématiques
Catégories : Algorithme | Matrice
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Algorithme de Coppersmith–Winograd de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Algorithme De Coppersmith-Winograd — L’algorithme de Coppersmith Winograd est un algorithme de calcul du produit de deux matrices carrées de taille n du à Don Coppersmith et Shmuel Winograd en 1987[1]. Sa complexité algorithmique est en ce qui en fait l algorithme le plus efficace… … Wikipédia en Français
Algorithme de coppersmith-winograd — L’algorithme de Coppersmith Winograd est un algorithme de calcul du produit de deux matrices carrées de taille n du à Don Coppersmith et Shmuel Winograd en 1987[1]. Sa complexité algorithmique est en ce qui en fait l algorithme le plus efficace… … Wikipédia en Français
Algorithme de Coppersmith-Winograd — L’algorithme de Coppersmith Winograd est un algorithme de calcul du produit de deux matrices carrées de taille n dû à Don Coppersmith et Shmuel Winograd en 1987[1]. Sa complexité algorithmique est en ce qui en fait l algorithme actuel le plus… … Wikipédia en Français
Algorithme De Strassen — L’algorithme de Strassen est un algorithme calculant le produit de deux matrices carrées de taille n. Il est dû à Volker Strassen en 1969.[1] La complexité de l algorithme est en O(n2,807), soit une meilleure complexité que la multiplication… … Wikipédia en Français
Algorithme de strassen — L’algorithme de Strassen est un algorithme calculant le produit de deux matrices carrées de taille n. Il est dû à Volker Strassen en 1969.[1] La complexité de l algorithme est en O(n2,807), soit une meilleure complexité que la multiplication… … Wikipédia en Français
Algorithme de Strassen — L’algorithme de Strassen est un algorithme calculant le produit de deux matrices carrées de taille n. Il est dû à Volker Strassen en 1969[1]. La complexité de l algorithme est en O(n2,807), soit une meilleure complexité que la multiplication… … Wikipédia en Français
Algorithme De Karatsuba — L algorithme de Karatsuba (1960) est une méthode permettant de multiplier rapidement deux nombres avec une complexité en au lieu de O(n2) pour la méthode naïve. Note : . Sommaire 1 Énoncé … Wikipédia en Français
Algorithme De Multiplication — Les techniques de multiplication permettent de calculer le résultat d une multiplication. Graphiquement, il s agit de transformer un rectangle multiplicateur × multiplicande en une ligne, en conservant le nombre d éléments. Exemples: Sommaire 1… … Wikipédia en Français
Algorithme de karatsuba — L algorithme de Karatsuba (1960) est une méthode permettant de multiplier rapidement deux nombres avec une complexité en au lieu de O(n2) pour la méthode naïve. Note : . Sommaire 1 Énoncé … Wikipédia en Français
Algorithme de Toom-Cook — Algorithme Toom Cook Toom Cook, aussi appelé Toom 3, est une technique de multiplication utilisée pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on effectuera les calculs. Multiplier deux … Wikipédia en Français
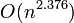 ce qui en fait l'algorithme le plus efficace en théorie. Rien n'indique que la complexité est optimale, l'exposant 2 étant généralement considéré comme optimal[2].
ce qui en fait l'algorithme le plus efficace en théorie. Rien n'indique que la complexité est optimale, l'exposant 2 étant généralement considéré comme optimal[2].