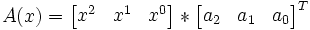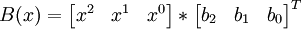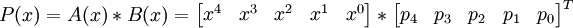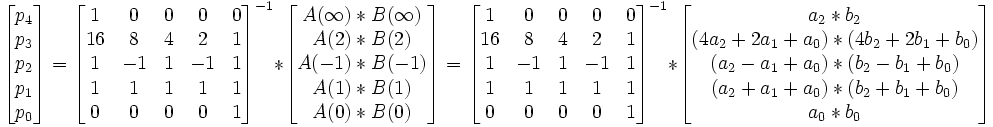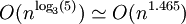Toom-Cook

Toom-Cook

Algorithme Toom-Cook

Toom-Cook, aussi appelé Toom-3, est une technique de multiplication utilisée pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on effectuera les calculs.

Multiplier deux nombres revient à multiplier deux polynômes

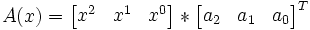
A(x) = \begin{bmatrix} x^2 & x^1 & x^0 \end{bmatrix} * \begin{bmatrix} a_2 & a_1 & a_0 \end{bmatrix}^T

et

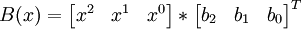
B(x) = \begin{bmatrix} x^2 & x^1 & x^0 \end{bmatrix} * \begin{bmatrix} b_2 & b_1 & b_0 \end{bmatrix}^T

ce qui donne un troisième polynôme

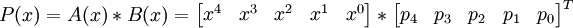
P(x) = A(x)*B(x) = \begin{bmatrix} x^4 & x^3 & x^2 & x^1 & x^0 \end{bmatrix} * \begin{bmatrix} p_4 & p_3 & p_2 & p_1 & p_0 \end{bmatrix}^T

En l'évaluant en cinq points

\begin{bmatrix} P(\infty) \\ P( 2) \\ P(-1) \\ P( 1) \\ P( 0) \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} p_4 \\ p_3 \\ p_2 \\ p_1 \\ p_0 \end{bmatrix}

ses coefficients peuvent être déterminés

\begin{bmatrix} p_4 \\ p_3 \\ p_2 \\ p_1 \\ p_0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{-1} * \begin{bmatrix} P(\infty) \\ P( 2) \\ P(-1) \\ P( 1) \\ P( 0) \end{bmatrix}

Ce calcul nécessite cinq multiplications trois fois plus simples et quelques additions

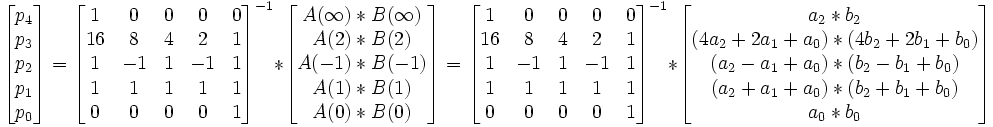
\begin{bmatrix} p_4 \\ p_3 \\ p_2 \\ p_1 \\ p_0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{-1} * \begin{bmatrix} A(\infty)*B(\infty) \\ A( 2)*B( 2) \\ A(-1)*B(-1) \\ A( 1)*B( 1) \\ A( 0)*B( 0) \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 16 & 8 & 4 & 2 & 1 \\ 1 & -1 & 1 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{-1} * \begin{bmatrix} a_2*b_2 \\ (4a_2+2a_1+a_0)*(4b_2+2b_1+b_0) \\ (a_2-a_1+a_0)*(b_2-b_1+b_0) \\ (a_2+a_1+a_0)*(b_2+b_1+b_0) \\ a_0*b_0 \end{bmatrix}

La complexité est donc

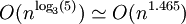
O(n^{\log _3 (5)}) \simeq O(n^{1.465})

Voir aussi

Références

  • Тоом Андрей Леонович, О сложности схемы из функциональных элементов, реализующей умножение целых чисел, Доклады Академии Наук СССР, T.150, N°3, pagg.496-498 [1]
  • D. Knuth. The Art of Computer Programming, Volume 2. Troisième édition, Addison-Wesley, 1997.
  • R. Crandall & C. Pomerance. Prime Numbers - A Computational Perspective. Seconde édition, Springer, 2005.
  • Toom 3-Way Multiplication, documentation de GMP
Algorithmes de multiplication
Produit de matrices Naïf  · Strassen  · Coppersmith-Winograd
Produit d'entiers Naïf  · Karatsuba  · Toom-Cook  · Schönhage-Strassen  · Fürer
Ce document provient de « Algorithme Toom-Cook ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Toom-Cook de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Toom–Cook multiplication — Toom–Cook, sometimes known as Toom 3, named after Andrei Toom and Stephen Cook, is a multiplication algorithm, a method of multiplying two large integers.Given two large integers, a and b , Toom–Cook splits up a and b into k smaller parts each of …   Wikipedia

  • Toom-Cook-Algorithmus — Der Toom Cook Algorithmus ist ein effizienter Algorithmus zur Multiplikation zweier ganzer Zahlen, der nach dem Prinzip Teile und herrsche arbeitet. Er wurde zuerst von Andrei Toom beschrieben, später durch Cook verbessert und in dessen… …   Deutsch Wikipedia

  • Algorithme de Toom-Cook — Algorithme Toom Cook Toom Cook, aussi appelé Toom 3, est une technique de multiplication utilisée pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on effectuera les calculs. Multiplier deux …   Wikipédia en Français

  • Algorithme Toom-Cook — L algorithme de Toom Cook, aussi appelé Toom 3, est un algorithme de multiplication dû à Andrei Toom (en) et Stephen Cook, utilisé pour multiplier deux grands nombres. Ces grands nombres sont découpés en plus petits nombres sur lesquels on… …   Wikipédia en Français

  • Toom — may refer to:* Andrei Toom (born 1942), Russian mathematician * Toom–Cook multiplication or Toom 3, a mathematical algorithm * Toom (Netherlands), a hamlet * Toom (supermarket), a chain of supermarkets in Germany * Toum, a garlic sauce from… …   Wikipedia

  • Andrei Toom — Andrei Toom, also known as André Toom, (born 1942) is a Russian mathematician currently living in Brazil, famous for his early work in analysis of algorithms (culminating in the Toom–Cook algorithm), cellular automata, probability theory and… …   Wikipedia

  • Stephen A. Cook — 2008 Stephen Arthur Cook (* 14. Dezember 1939 in Buffalo, New York) ist Professor der Informatik an der University of Toronto in Kanada. Sein Hauptbetätigungsfeld ist die Komplexitätstheorie; Cook arbeitet neben seiner Lehrtätigkeit aber auch an… …   Deutsch Wikipedia

  • Multiplication algorithm — A multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are in use. Efficient multiplication algorithms have existed since the advent of the decimal system.… …   Wikipedia

  • Computational complexity of mathematical operations — The following tables list the running time of various algorithms for common mathematical operations. Here, complexity refers to the time complexity of performing computations on a multitape Turing machine.[1] See big O notation for an explanation …   Wikipedia

  • Karatsuba-Algorithmus — Der Karatsuba Algorithmus (1960) ist ein Algorithmus zur Multiplikation zweier ganzer Zahlen. Mit einer Laufzeitkomplexität von ist er deutlich schneller als der naive Algorithmus nach der Schulmethode. Dieser (und auch dessen implizite… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”