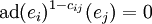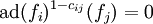Algebre de Kac-Moody

Algebre de Kac-Moody: Algèbre de Kac-Moody

En mathématiques, une algèbre de Kac-Moody est une algèbre de Lie, généralement de dimension infinie, pouvant être définie par des générateurs et des relations via une matrice de Cartan généralisée. Les algèbres de Kac-Moody tiennent leur nom de Victor Kac et de Robert Moody, qui les ont indépendamment découvert. Ces algèbres sont une généralisation des algèbres semi-simples de Lie de dimension finie, et de nombreuses propriétés liées à la structure des algèbres de Lie, notamment son système de racines, ses représentations irréductibles, ses liens avec les variétés de drapeaux ont des équivalents dans le système de Kac-Moody. Une classe d'algèbres de Kac-Moody appelée algèbre de Lie affine est particulièrement importante dans les mathématiques et la physique théorique, et plus spécifiquement dans les théories conforme des champs et des modèles exactement solubles. Kac démontra élégamment certaines identités combinatoires, les identités de Macdonald, en se basant sur la représentation théorique d'algèbres de Kac-Moody affines. Garland et Lepowski démontrèrent quant à eux que les identités de Rogers-Ramanujan pouvaient être dérivées de façon similaire.

Sommaire

1 Definition

2 Interprétation

3 Types d'algèbres de Kac-Moody

4 References

Definition

Une algèbre de Kac-Moody est déterminée comme suit :

Une matrice de Cartan généralisée de taille 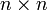$n \times n$ , $C = (c i j)$ de rang r.

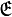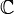Un espace vectoriel $\mathfrak{E}$ sur $\Complex$ de dimension 2n - r.

Un ensemble de n vecteurs libres $α i$ de 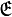$\mathfrak{E}$ et un ensemble de n vecteurs libres 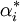$\alpha_i^*$ de l'espace dual associé à 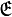$\mathfrak{E}$ , tel que 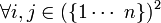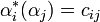$\forall{i,j}\in(\{1\cdots\ n\})^2$ , $\alpha_i^*(\alpha_j) = c_{ij}$ . Les $α i$ sont appelés coracines, tandis que les 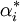$\alpha_i^*$ sont appelés racines.

L'algèbre de Kac-Moody est l'algèbre de Lie 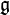$\mathfrak{g}$ définie par les vecteurs générateurs $e i$ et $f i$ et les éléments de 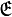$\mathfrak{E}$ ainsi que les relations :

$[e_i,f_i] = \alpha_i \$

$\forall{i} \neq j, [e_i,f_j] = 0$

$\forall{x}\in\mathfrak{E} , [e_i,x]=\alpha_i^*(x)e_i$

$\forall{x}\in\mathfrak{E} , [f_i,x]=-\alpha_i^*(x)f_i$

$\forall{x,x'}\in\mathfrak{E}, [x,x'] = 0$

$\textrm{ad}(e_i)^{1-c_{ij}}(e_j) = 0$

$\textrm{ad}(f_i)^{1-c_{ij}}(f_j) = 0$

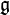Où $\textrm{ad}: \mathfrak{g}\to\textrm{gl}(\mathfrak{g}),\textrm{ad}(x)(y)=[x,y]$ est la représentation adjointe de $\mathfrak{g}$ .

Une algèbre de Lie (de dimension infinie ou non) sur le corps des réels est également considérée comme une algèbre de Kac-Moody si sa complexification est une algèbre de Kac-Moody.

Interprétation

Soit 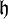$\mathfrak{h}$ une sous-algèbre de Cartan de l'algèbre de Kac-Moody.

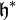Si g est un élément de l'algèbre de Kac-Moody tel que $\forall{x}\in\mathfrak{h}, [g,x]=\omega(x)g$ , où $ω$ est un élément de $\mathfrak{h}^*$ , alors on dit que g a un poids $ω$ . L'algèbre de Kac-Moody peut être diagonalisée en vecteurs propres de poids. La sous-algèbre de Cartan 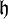$\mathfrak{h}$ a un poids nul, $e i$ a un poids 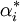$\alpha_i^*$ et $f i$ a un poids 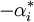$-\alpha_i^*$ . Si le crochet de Lie de deux vecteurs propres est non nul, alors son poids est la somme de leurs poids. 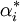La condition $[e_i,f_i] = 0\ \forall{i}\neq{j}$ signifie simplement que les $\alpha_i^*$ sont des racines simples.

Types d'algèbres de Kac-Moody

La matrice de Cartan associée à l'algèbre de Kac-Moody 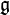$\mathfrak{g}$ peut être décomposée comme produit de deux matrices D et S où D est une matrice diagonale positive et S une matrice symétrique. La nature de S détermine le type de l'algèbre de Kac-Moody dont il est question :

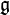$\mathfrak{g}$ est une algèbre de Lie simple de dimension finie si S est définie positive

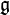$\mathfrak{g}$ est affine si S est semi-définie positive de corang 1

Il existe aussi une autre classe d'algèbre de Kac Moody appelée algèbres hyperboliques. S ne peut jamais être définie négative ou semi-définie négative puisque ses coefficient diagonaux sont positifs.

Ces types d'algèbres de Kac Moody sont également caractérisés par leurs diagrammes de Dynkin:

on connait la liste exacte des diagrammes de Dynkin correspondant aux algèbres de Lie simples

lorsque tout sous diagramme du diagramme de Dynkin de 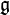$\mathfrak{g}$ est le diagramme d'une algèbre de Lie simple, alors 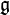$\mathfrak{g}$ est affine

lorsque tout sous diagramme du diagramme de Dynkin de 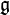$\mathfrak{g}$ est le diagramme d'une algèbre affine, alors 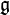$\mathfrak{g}$ est hyperbolique

Les algèbres affines sont les mieux connues des algèbres de Kac-Moody.

References

A. J. Wassermann, Comptes rendus de lectures sur les algèbres de Kac-Moody et de Virasoro

V. Kac Infinite dimensional Lie algebras ISBN 0-521-46693-8

Hazewinkel, Michiel, ed. (2001), "Kac–Moody algebra", (en) Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1-55608-010-4

V.G. Kac, Simple irreducible graded Lie algebras of finite growth Math. USSR Izv. , 2 (1968) pp. 1271–1311 Izv. Akad. Nauk USSR Ser. Mat. , 32 (1968) pp. 1923–1967

R.V. Moody, A new class of Lie algebras J. of Algebra , 10 (1968) pp. 211–230

Portail des mathématiques

Ce document provient de « Alg%C3%A8bre de Kac-Moody ».

Catégorie : Algèbre de Lie

Contenu soumis à la licence CC-BY-SA. Source : Article Algebre de Kac-Moody de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Algèbre de Kac-Moody — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre de Kac Moody est une algèbre de Lie, généralement de dimension infinie, pouvant être définie par des générateurs et des relations via une matrice de Cartan… … Wikipédia en Français
Algebre de Lie — Algèbre de Lie En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1 … Wikipédia en Français
Algèbre De Lie — En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1.1 Définition … Wikipédia en Français
Algèbre de lie — En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1.1 Définition … Wikipédia en Français
Algèbre de Lie — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d un crochet de Lie, c est à dire d une loi de composition interne… … Wikipédia en Français
Kac — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sigles d’une seule lettre Sigles de deux lettres > Sigles de trois lettres Sigles de quatre lettres … Wikipédia en Français
Algèbre (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot « algèbre » vient de l arabe ’al ǧabr (« réduction »), désignant une technique de chirurgie des membres puis une technique de… … Wikipédia en Français
Algebre vertex — Algèbre vertex En mathématiques, une algèbre vertex est une structure algébrique qui joue un rôle important en théorie conforme des champs et dans les domaines proches en physique. Ces structures ont aussi montré leur utilité en mathématiques… … Wikipédia en Français
Algèbre Vertex — En mathématiques, une algèbre vertex est une structure algébrique qui joue un rôle important en théorie conforme des champs et dans les domaines proches en physique. Ces structures ont aussi montré leur utilité en mathématiques dans des contextes … Wikipédia en Français
Algèbre vertex — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre vertex est une structure algébrique qui joue un rôle important en théorie conforme des champs et dans les domaines proches en physique. Ces structures ont aussi… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts