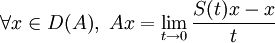Hille Yosida

Théorème de Hille-Yosida

En théorie des semi-groupes, le théorème de Hille-Yosida est un outil puissant et fondamental reliant les propriétés de dissipation de l'énergie d'un opérateur non borné $A : D(A) \subset X \longrightarrow X$ à l'existence-unicité et la régularité des solutions d'une équation différentielle (E) $\begin{cases} x'(t) = Ax(t) \\ x(0) = x_0 \end{cases}$ .

Sommaire

1 Semi-groupes
- 1.1 Définitions
- 1.2 Propriétés des semi-groupes de contraction
2 Opérateurs dissipatifs
- 2.1 Définitions
- 2.2 Propriétés des opérateurs m-dissipatifs
3 Théorème de Hille-Yosida
- 3.1 Enoncé
- 3.2 Régularité des solutions
4 Exemples
- 4.1 L'équation de la chaleur
- 4.2 L'équation des ondes

Semi-groupes

La théorie des semi-groupes doit son origine à l'étude du flot d'une équation différentielle ordinaire autonome en dimension finie ainsi que de l'exponentielle d'opérateurs.

Définitions

Soit $X$ un espace de Banach; on dit que la famille d'opérateurs linéaires 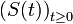$\left(S(t)\right)_{t\geq0}$ est un semi-groupe (fortement continu) si :

(i)

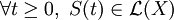
$\forall t\geq 0, ~ S(t)\in\mathcal{L}(X)$

(i i)

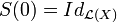
$S(0) = Id_{\mathcal{L}(X)}$

(i i i)

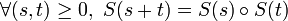
$\forall (s,t) \geq 0, ~ S(s+t) = S(s) \circ S(t)$

(i v)

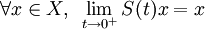
$\forall x \in X, ~ \lim_{t \rightarrow 0^+}S(t)x=x$

La condition $(i v)$ est équivalente à ce que 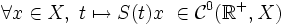$\forall x\in X, ~ t \mapsto S(t)x ~ \in \mathcal{C}^0(\mathbb{R}^+,X)$ . Si on remplace $(i v)$ par $(i v) *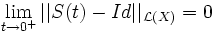$ : $\lim_{t \rightarrow 0^+}||S(t)-Id||_{\mathcal{L}(X)}=0$ on dit que 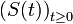$\left(S(t)\right)_{t\geq0}$ est uniformément continu.

On retrouve (vaguement) avec cette définition la notion de famille à un paramètre de difféomorphismes bien connue en théorie des EDO.

On définit le générateur infinitésimal $(A, D (A))$ d'un un semi-groupe fortement continu 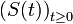$\left(S(t)\right)_{t \geq 0}$ comme l'opérateur non borné $A : D(A) \subset X \longrightarrow X$ où:

$D(A)=\{ x\in X, ~ \lim_{t \rightarrow 0} \frac{S(t)x -x}{t} \text{ existe}\}$

$\forall x \in D(A), ~ Ax = \lim_{t \rightarrow 0} \frac{S(t)x -x}{t}$

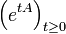Dans le cas où $D (A) = X$ et $A \in \mathcal{L}(X)$ la famille d'opérateurs $\left(e^{tA}\right)_{t \geq 0}$ (définie classiquement par sa série) est un semi-groupe fortement continu de générateur infinitésimal $A$ : c'est pourquoi on note parfois abusivement $S (t) = e t A$ .

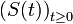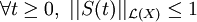On dit que le semi-groupe $\left(S(t)\right)_{t\geq0}$ est de contraction si $\forall t \geq 0, ~ ||S(t)||_{\mathcal{L}(X)}\leq 1$ .

Propriétés des semi-groupes de contraction

Théorème 1: soit $X$ un espace de Banach, 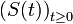$\left(S(t)\right)_{t\geq0}$ un semi-groupe de contraction sur $X$ et $(A, D (A))$ son générateur infinitésimal. Alors:

(i)

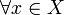$\forall x \in X$ le flot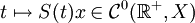 $t \mapsto S(t)x \in \mathcal{C}^0(\mathbb{R}^+,X)$

(i i)

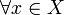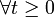
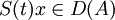$\forall x \in X$ et $\forall t \geq 0$ $S(t)x \in D(A)$ , le flot $t \mapsto S(t)x \in \mathcal{C}^1(\mathbb{R}^+,X)$ et vérifie

x'(t) = A x (t)

(i i i)

(A, D (A))

est fermé de domaine dense.

Théorème 2 (caractérisation des générateurs infinitésimaux): soit $A : D(A) \subset X \longrightarrow X$ un opérateur non borné sur $X$ . On a l'équivalence:

(i)

(A, D (A))

est le générateur infinitésimal d'un semi-groupe de contraction

(i i)

D (A)

est dense et pour toute condition initiale 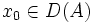$x_0 \in D(A)$ il existe une unique solution 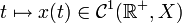$t \mapsto x(t) \in \mathcal{C}^1(\mathbb{R}^+,X)$ de (E).

De plus sous cette hypothèse la solution $x (t)$ est à valeurs dans $D (A)$ et vérifie $||x(t)||_X \leq ||x_0||_X$ ainsi que $||x'(t)||_X \leq ||Ax(t)||_X \leq ||Ax_0||_X$ (inégalités d'énergie).

On commence à voir apparaître le lien entre le problème (E) et la notion de semi-groupe. Pour préciser, il faut maintenant introduire la notion d'opérateur dissipatif.

Opérateurs dissipatifs

Définitions

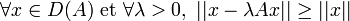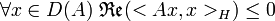Un opérateur $(A, D (A))$ est dissipatif si $\forall x\in D(A) \text{ et } \forall \lambda >0, ~ ||x-\lambda Ax|| \geq ||x||$ . Dans le cas où $X = H$ est hilbertien on montre que $A$ est dissipatif si et seulement si $\forall x\in D(A) ~ \mathfrak{Re}(<Ax,x>_H) \leq 0$ .

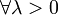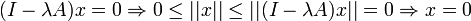Remarque: Si $(A, D (A))$ est un opérateur dissipatif alors $\forall \lambda > 0$ l'opérateur $(I d - λ A)$ est injectif car $(I-\lambda A)x = 0 \Rightarrow 0 \leq ||x|| \leq ||(I-\lambda A)x||=0 \Rightarrow x= 0$ .

Si de plus 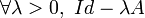$\forall \lambda >0, ~ Id - \lambda A$ est surjectif on dit que $(A, D (A))$ est maximal-dissipatif (ou m-dissipatif). On peut montrer que 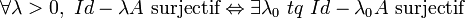$\forall \lambda >0, ~ Id - \lambda A ~ \text{surjectif} \Leftrightarrow \exists \lambda_0 ~ tq ~ Id - \lambda_0 A ~ \text{surjectif}$ . En pratique pour montrer qu'un opérateur est m-dissipatif on montre d'abord à la main qu'il est dissipatif et on résout ensuite un problème variationnel pour une valeur $λ 0$ bien choisie (par exemple avec le théorème de Lax-Milgram, voir exemple de l'équation de la chaleur traité plus bas).

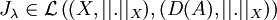Dans ce cas l'opérateur $(I d - λ A)$ est un isomorphisme (a priori non continu) de $L (A, X)$ et on note $J λ = (I d - λ A) - 1$ . De plus, comme $||J_{\lambda}y||_X \leq ||(Id-\lambda A)[J_{\lambda}y]||_X \leq ||y||_X$ , $J_{\lambda} \in \mathcal{L}\left((X,||.||_X),(D(A),||.||_X)\right)$ . Nous allons voir que cette propriété de continuité peut être améliorée (on va rendre moins fine la topologie sur $(D (A), | | . | | X)$ en munissant $D (A)$ d'une norme $| | . | | D (A)$ ).

Propriétés des opérateurs m-dissipatifs

Prop 1: si $(A, D (A))$ est m-dissipatif alors c'est un opérateur fermé.

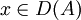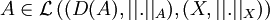Corollaire 1: pour $x \in D(A)$ on pose $| | x | | D (A) = | | x | | X + | | A x | | X$ . Alors $| | . | | D (A)$ est une norme pour laquelle $D (A)$ est un espace de Banach et $A \in \mathcal{L}\left((D(A),||.||_A),(X,||.||_X)\right)$ .

Prop 2: si $H$ est un espace Hilbertien et 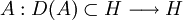$A : D(A) \subset H \longrightarrow H$ est m-dissipatif alors il est à domaine dense.

Prop 3: réciproquement si 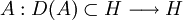$A : D(A) \subset H \longrightarrow H$ est de domaine dense, dissipatif, fermé et tel que son adjoint $(A *, D (A *))$ est dissipatif alors $(A, D (A))$ est m-dissipatif.

Corollaire 3: toujours dans le cadre hilbertien

(i)

(A, D (A))

est dissipatif autoadjoint à domaine dense alors il est m-dissipatif

(i i)

(A, D (A))

est antioadjoint à domaine dense alors il est m-dissipatif

Remarque: dans $(i i)$ la condition de dissipativité n'est pas nécessaire car $(A, D (A))$ autoadjoint entraîne que $< A x, x > H = 0$ donc la dissipativité, voir l'exemple de l'équation des ondes plus bas.

Théorème de Hille-Yosida

Enoncé

Théorème 3 (Hille-Yosida): soit $X$ un espace de Banach et $A : D(A) \subset X \longrightarrow X$ un opérateur non borné. On a l'équivalence

(i)

(A, D (A))

est m-dissipatif à domaine dense

(i i)

(A, D (A))

est le générateur infinitésimal d'un semi-groupe de contraction

Le point $(i)$ du théorème précédent peut être réécrit en termes de résolvante : $(i')$ $(A, D (A))$ , opérateur fermé à domaine dense, vérifie 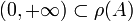$(0,+\infty) \subset \rho(A)$ et $\forall \lambda > 0 \; \|R_\lambda\| \leq \frac{1}{\lambda}$ .

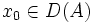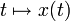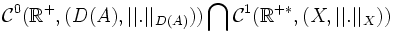Ainsi sous ces hypothèses et d'après le théorème 2 pour toute condition initiale $x_0 \in D(A)$ il existe une unique solution forte $t \mapsto x(t)$ dans $\mathcal{C}^0(\mathbb{R}^+,(D(A),||.||_{D(A)})) \bigcap \mathcal{C}^1(\mathbb{R}^{+*},(X,||.||_X))$ . Lorsque la condition initiale est prise quelconque dans $X$ on a une solution faible 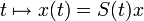$t \mapsto x(t) = S(t)x$ de classe seulement $\mathcal{C}^0(\mathbb{R}^+,(X,||.||_X))$ ( et on montre que toute solution faible est limite dans $X$ de solutions fortes).

Régularité des solutions

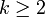
On constate que la régularité de la solution est étroitement liée au choix de la condition initiale en fonction du domaine de A: il est donc naturel de penser qu'en imposant plus de "régularité" à $x 0$ on obtienne plus de régularité sur les solutions. Plus précisément on pose pour 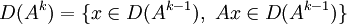$k \geq 2$ $D(A^k)=\{x \in D(A^{k-1}), ~ Ax \in D(A^{k-1})\}$ . Alors on a le

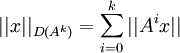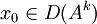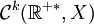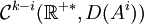Théorème 4: on peut munir les $D (A k)$ des normes $||x||_{D(A^k)}=\sum_{i=0}^k ||A^ix||$ pour lesquels ce sont des espaces de Banach. De plus si la condition initiale $x_0 \in D(A^k)$ alors la solution est de classe $\mathcal{C}^k(\mathbb{R}^{+*},X)$ et $\mathcal{C}^{k-i}(\mathbb{R}^{+*},D(A^i))$ pour $i = 1... k$ et au sens des topologies précédentes.

Exemples

L'équation de la chaleur

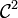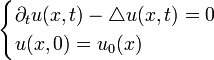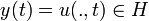On se donne $Ω$ un ouvert borné de classe $\mathcal{C}^2$ de $\mathbb{R}^n$ et on cherche à résoudre l'équation de la chaleur $\begin{cases} \partial_t u(x,t) - \triangle u(x,t)=0 \\ u(x,0) = u_0(x) \end{cases}$ sur $(x,t)\in \Omega \times [0,+\infty]$ pour une condition initiale donnée. 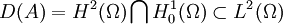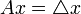On peut réécrire cette EDP sous la forme d'une EDO $y'(t) = A y (t)$ en posant $X = H = L 2 (Ω)$ , $y(t)=u(.,t)\in H$ et en définissant $(A, D (A))$ par $D(A)=H^2(\Omega) \bigcap H^1_0(\Omega) \subset L^2(\Omega)$ et $Ax=\triangle x$ pour tout 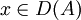$x \in D(A)$ . Nous sommes dans le bon cadre pour utiliser la théorie des semi-groupes et le théorème de Hille-Yosida; reste à montrer que l'opérateur A est m-dissipatif. Il est bien connu que le laplacien est un opérateur autoadjoint (on a $<Au,v>_H=\int_{\Omega}(\triangle u)v = -\int_{\Omega}\nabla u . 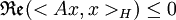\nabla v=\int_{\Omega}u(\triangle v ) = <u,Av>_H$ par double intégration par parties) et que $D (A)$ est dense dans $L 2 (Ω)$ , il suffit donc de montrer qu'il est dissipatif ou de façon équivalente que $\mathfrak{Re}(<Ax,x>_H) \leq 0$ . 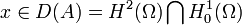Or tout $x \in D(A)=H^2(\Omega) \bigcap H^1_0(\Omega)$ est de trace nulle, donc en intégrant par parties 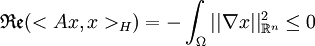$\mathfrak{Re}(<Ax,x>_H)=-\int_{\Omega}||\nabla x||^2_{\mathbb{R}^n} \leq 0$ . Le corollaire 3 et le théorème de Hille-Yosida permettent enfin de conclure quant à l'existence-unicité et la régularité des solutions. Remarquer que 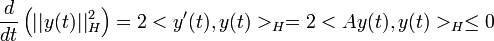$\frac{d}{dt}\left(||y(t)||^2_H\right)=2<y'(t),y(t)>_H=2<Ay(t),y(t)>_H \leq 0$ : on retrouve bien sur le côté dissipatif et irréversible de l'équation de la chaleur.

L'équation des ondes

L'équation des ondes homogène se formule dans un domaine $Ω$ suffisamment régulier (c'est-à-dire $\mathcal{C}^2$ en pratique) et sur un intervalle de temps $[0, T)$ (avec $T > 0$ ) selon

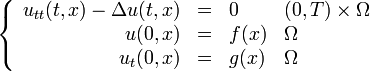
$\left\{\begin{array}{rcll}u_{tt}(t,x) -\Delta u(t,x) & = & 0 & (0,T) \times \Omega\\ u(0,x) & = & f(x) & \Omega\\ u_{t}(0,x) & = & g(x) & \Omega \end{array}\right.$

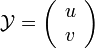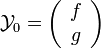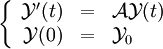On se place dans la théorie des semi-groupes en mettant l'équation précédente au premier ordre en temps. On pose alors $\mathcal{A} = \left(\begin{array}{cc} 0 & I \\ \Delta & 0 \end{array}\right)$ , $\mathcal{Y} = \left(\begin{array}{c} u \\ v \end{array}\right)$ (avec $v = u'$ ) et $\mathcal{Y}_0 = \left(\begin{array}{c} f \\ g \end{array}\right)$ l'équation devient alors $\left\{\begin{array}{rcll} \mathcal{Y}'(t) & = & \mathcal{A}\mathcal{Y}(t) \\ \mathcal{Y}(0) & = & \mathcal{Y}_0 \end{array}\right.$ .

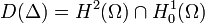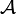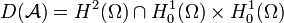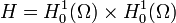Le domaine du Laplacien étant $D(\Delta) = H^2(\Omega) \cap H_0^1(\Omega)$ , celui de $\mathcal{A}$ est $D(\mathcal{A}) = H^2(\Omega) \cap H_0^1(\Omega) \times H_0^1(\Omega)$ sur $H = H_0^1(\Omega) \times H_0^1(\Omega)$ . Les conditions initiales seront alors prises dans $H$ .

Reste à vérifier que nous sommes bien dans les conditions d'application du théorème de Hille-Yosida :

$D(\mathcal{A})$ est dense dans $H$ .
$\mathcal{A}$ est fermé.
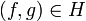$\mathcal{A}$ est dissipatif. Ce point mérite une preuve : on utilise la caractérisation $(i')$ du théorème. Soient $λ > 0$ et $(f,g) \in H$ . L'équation résolvante s'écrit en $(u, v)$

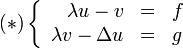$(*)\left\{ \begin{array}{rcl} \lambda u - v & = & f \\ \lambda v - \Delta u & = & g \end{array} \right.$ d'où $(λ 2 I - Δ) u = λ f + g$ qui admet une unique solution dans $u \in H^1_0(\Omega)$ via Lax-Milgram (car d'une part $λ 2 > 0$ et d'autre part les valeurs propres du Laplacien sont strictement négatives donc $(λ 2 I - Δ)$ est un opérateur elliptique dont la forme bilinéaire associée vérifie les hypothèses du théorème de Lax-Milgram). 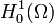Et alors $v = λ u - f$ est dans $H_0^1(\Omega)$ .

L'estimation de l'opérateur résolvant $R λ$ vient du produit scalaire de $( * ) 2$ par $v$ en remplaçant $u$ par sa valeur dans $( * ) 1$ :

$\begin{array}{rcl} \lambda (\|v\|_{L^2(\Omega)} + \|\nabla u\|_{L^2(\Omega)}) & =& ( \nabla f,\nabla u)_{L^2(\Omega)} + (g, v)_{L^2(\Omega)} \\ & \leq & (\|g\|_{L^2(\Omega)}^2 + \|\nabla f\|_{L^2(\Omega)}^2)^{1/2}(\|v\|_{L^2(\Omega)}^2+\|\nabla u\|_{L^2(\Omega)}^2)^{1/2}. \end{array}$

D'où, puisque $(u, v) = R λ (f, g)$ , on obtient l'estimation attendue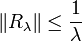 $\|R_\lambda\| \leq \frac{1}{\lambda}$ . Le semi-groupe engendré par 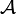$\mathcal{A}$ est donc un semi-groupe de contraction.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Hille-Yosida ».

Catégorie : Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hille Yosida de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Hille–Yosida theorem — In functional analysis, the Hille–Yosida theorem characterizes one parameter semigroups of linear operators on Banach spaces satisfying certain continuity restrictions. The theorem is useful for solving certain differential equations such as the… … Wikipedia
Theoreme de Hille-Yosida — Théorème de Hille Yosida En théorie des semi groupes, le théorème de Hille Yosida est un outil puissant et fondamental reliant les propriétés de dissipation de l énergie d un opérateur non borné à l existence unicité et la régularité des… … Wikipédia en Français
Théorème de Hille-Yosida — En théorie des semi groupes, le théorème de Hille Yosida est un outil puissant et fondamental reliant les propriétés de dissipation de l énergie d un opérateur non borné à l existence unicité et la régularité des solutions d une équation… … Wikipédia en Français
Satz von Hille-Yosida — Eine stark stetige Halbgruppe (gelegentlich auch als C0 Halbgruppe bezeichnet) ist eine Familie von stetigen linearen Abbildungen eines reellen oder komplexen Banachraums X in sich, welche die drei Eigenschaften T(0) = I, T(s + t) = T(s)T(t) für… … Deutsch Wikipedia
Yosida — Kōsaku Yosida (1969) Kōsaku Yosida (jap. 吉田耕作, Yoshida Kōsaku; * 7. Februar 1909 in Hiroshima, Japan, † 20. Juni 1990) war ein japanischer Mathematiker, der durch seine Arbeiten in der Funktionalanalysis bekannt geworden ist. Yosida studierte an … Deutsch Wikipedia
Hille — *Bertil Hille, Biologist *David Hille Footballer *Einar Carl Hille, Mathematician *Veda Hille, singer * Hille, Germany Town * Hille–Yosida theorem in mathematics … Wikipedia
Kosaku Yosida — Kōsaku Yosida (1969) Kōsaku Yosida (jap. 吉田耕作, Yoshida Kōsaku; * 7. Februar 1909 in Hiroshima, Japan, † 20. Juni 1990) war ein japanischer Mathematiker, der durch seine Arbeiten in der Funktionalanalysis bekannt geworden ist. Yosida studierte an … Deutsch Wikipedia
Kôsaku Yosida — Kōsaku Yosida (1969) Kōsaku Yosida (jap. 吉田耕作, Yoshida Kōsaku; * 7. Februar 1909 in Hiroshima, Japan, † 20. Juni 1990) war ein japanischer Mathematiker, der durch seine Arbeiten in der Funktionalanalysis bekannt geworden ist. Yosida studierte an … Deutsch Wikipedia
Einar Carl Hille — Einar Hille (birth name Carl Einar Hille) was an American mathematician,born 28 June 1894 in New York, USA, and died 12 February 1980 in La Jolla, California.Hille s main work was on integral equations, differential equations, special functions,… … Wikipedia
Kōsaku Yosida — (1969) Kōsaku Yosida (jap. 吉田耕作, Yoshida Kōsaku; * 7. Februar 1909 in Hiroshima, Japan; † 20. Juni 1990) war ein japanischer Mathematiker, der durch seine Arbeiten in der Funktionalanalysis bekannt … Deutsch Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Hille Yosida

Théorème de Hille-Yosida

Sommaire

Semi-groupes

Définitions

Propriétés des semi-groupes de contraction

Opérateurs dissipatifs

Définitions

Propriétés des opérateurs m-dissipatifs

Théorème de Hille-Yosida

Enoncé

Régularité des solutions

Exemples

L'équation de la chaleur

L'équation des ondes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Hille Yosida

Théorème de Hille-Yosida

Sommaire

Semi-groupes

Définitions

Propriétés des semi-groupes de contraction

Opérateurs dissipatifs

Définitions

Propriétés des opérateurs m-dissipatifs

Théorème de Hille-Yosida

Enoncé

Régularité des solutions

Exemples

L'équation de la chaleur

L'équation des ondes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link